【论文笔记】Re-ranking

文章基本信息

• 文章名称：Re-ranking Person Re-identification with k-reciprocal Encoding
• 发表会议/年份：CVPR 2017
• 作者：Zhun Zhong, Liang Zheng, Donglin Cao, Shaozi Li
• 单位：Cognitive Science Department, Xiamen University, China / University of Technology Sydney / Fujian Key Laboratory of Brain-inspired Computing Technique and Applications, Xiamen University

摘要

在将人员重新识别（Re-ID）视为检索过程时，重排名是提高其准确性的重要步骤。然而，在Re-ID领域，投入到重排名上的努力有限，尤其是那些完全自动化的、无监督的解决方案。在本文中，我们提出了一种k-互惠编码方法来重新排名Re-ID的结果。我们的假设是，如果图库图像在k-互惠最近邻中与探针图像相似，那么它更有可能是真正的匹配。具体来说，给定一张图像，通过将其k-互惠最近邻编码为单个向量来计算k-互惠特征，该向量用于基于Jaccard距离的重新排名。最终距离计算为原始距离和Jaccard距离的组合。我们的重排名方法不需要任何人工干预或标记数据，因此适用于大规模数据集。在大规模Market-1501、CUHK03、MARS和PRW数据集上的实验结果证实了我们方法的有效性。

之前工作存在的问题

过往的重排名方法依赖于初始排名列表的质量，通过利用初始排名列表中高排名图像之间的相似关系进行重排名。然而，这些方法存在以下问题：

1. 初始排名列表中可能包含错误匹配，这些错误匹配可能会被误认为是真正的匹配，从而影响重排名的准确性；
2. 即使真正的匹配存在，它们也可能不会出现在初始排名列表的前几名，从而导致重排名时的噪声增加，最终结果被破坏。

比如如上图1所示，在图1中，P1、P2、P3和P4是探针的四个真正匹配，但它们都不在前四名排名中。我们观察到一些错误匹配（N1-N6）获得了高排名。因此，直接使用前k名排名图像可能会在重排名系统中引入噪声，影响最终结果。

主要贡献/创新

本文介绍了一种基于k-互惠近邻的重新排名方法，用于改进图像重新识别（re-ID）系统的性能。通过将加权的k-互惠邻居集编码为向量，计算图像之间的Jaccard距离，并结合局部查询扩展方法，最终得到改进的重新排名列表。该方法无需人工交互或标注数据，且能自动且无监督地应用于人重新识别排名，显著提高了多个数据集上的重新识别性能。

本文的贡献可以概括如下：

• 我们提出了通过将k-互惠特征编码为一个向量的k-互惠特征。重新排名过程可以通过向量比较轻松完成。
• 我们的方法不需要任何人工交互或标注数据，可以自动且无监督地应用于任何人重新识别排名结果。
• 所提出的方法有效提高了多个数据集上的人重新识别性能，包括Market-1501、CUHK03、MARS和PRW。特别是在Market-1501数据集上，我们在rank-1和mAP上都达到了最先进的精度。

方法

问题定义

给定一个探测者p和包含N幅图像的图库集合$\mathcal{G} = \{ g_i \mid i = 1, 2, \ldots, N \}$，两个人物p和$g_i$之间的原始距离可以通过马氏距离（Mahalanobis distance）来测量：

$$d(p, g_i) = (x_p - x_{g_i})^\top \mathbf{M} (x_p - x_{g_i})$$

其中$x_p$和$x_{g_i}$分别是人物p和$g_i$的特征向量，$\mathbf{M}$是一个正定矩阵。

初始排名列表 $\mathcal{L}(p, \mathcal{G}) = \{g_1^0, g_2^0, \ldots, g_N^0\}$ 可以根据探测者 $p$ 和图库 $g_i$ 之间的成对原始距离获得，其中 $d(p, g_i^0) < d(p, g_{i+1}^0)$。我们的目标是重新排序 $\mathcal{L}(p, \mathcal{G})$，以使更多的正样本排在列表的顶部，从而提高人物重新识别（re-ID）的性能。

K-reciprocal Nearest Neighbors

按照(35)，我们将 $N(p, k)$ 定义为探测者 $p$ 的k-近邻（即排名列表的前k个样本）：

$$N(p, k) = \{g_1^0, g_2^0, \ldots, g_k^0\}, \quad |N(p, k)| = k$$

其中 $|\cdot|$ 表示集合中候选项的数量。k-互惠近邻 $\mathcal{R}(p, k)$ 可以定义为：

$$\mathcal{R}(p, k) = \{ g_i \mid (g_i \in N(p, k)) \land (p \in N(g_i, k)) \}$$

根据之前的描述，k-互惠近邻与探测者 $p$ 的关系比k-近邻更密切。然而，由于光照、姿势、视角和遮挡的变化，正样本可能被排除在k-近邻之外，进而不包含在k-互惠近邻中。为了解决这个问题，我们通过逐步将$\mathcal{R}(p, k)$中每个候选项的 $\frac{1}{2}k$ 互惠近邻添加到一个更鲁棒的集合 $\mathcal{R}^*(p, k)$ 中来改进，依据如下条件：

$$\mathcal{R}^*(p, k) \leftarrow \mathcal{R}(p, k) \cup \mathcal{R}(q, \frac{1}{2}k)$$

条件是：

$$|\mathcal{R}(p, k) \cap \mathcal{R}(q, \frac{1}{2}k)| \geq \frac{2}{3} |\mathcal{R}(q, \frac{1}{2}k)|, \quad \forall q \in \mathcal{R}(p, k)$$

$q$是原本p的k近邻

通过这种操作，我们可以将更多与$\mathcal{R}(p, k)$ 中候选项更相似的正样本添加到$\mathcal{R}^*(p, k)$中，而不是与探测者 $p$ 更相似的样本。与（35）相比，这在防止包含过多负样本方面更为严格。

Jaccard距离

在本小节中，我们通过比较探测者 $p$ 和图库 $g_i$ 的k-互惠近邻集来重新计算它们之间的成对距离。如之前工作所述 (2) (46)，我们认为如果两幅图像相似，它们的k-互惠近邻集会有重叠，即在集合中存在一些重复的样本。重复样本越多，两幅图像就越相似。探测者 $p$ 和图库 $g_i$ 之间的新距离可以通过它们的k-互惠集的Jaccard度量来计算，公式如下：

$$d_J(p.g_i) = 1 - \frac{|\mathcal{R}^*(p,k)\cap\mathcal{R}^*(g_i,k)|}{|\mathcal{R}^*(p,k)\cup\mathcal{R}^*(g_i,k)|}$$

其中 $|\cdot|$ 表示集合中候选项的数量。我们采用Jaccard距离来命名这个新距离。尽管上述方法能够捕捉到两幅图像之间的相似关系，但仍存在三个明显的缺点：

1. 获取两个邻居集 $\mathcal{R}^*(p, k)$ 和 $\mathcal{R}^*(g_i, k)$ 的交集和并集在很多情况下是非常耗时的，并且当需要计算所有图像对的Jaccard距离时，这变得更加具有挑战性。一个替代方法是将邻居集编码为一个更简单但等效的向量，从而大大减少计算复杂度，同时保持邻居集中的原始结构。
2. 这种距离计算方法对所有邻居赋予了相同的权重，导致邻居集简单但缺乏辨别力。实际上，更接近探测者 $p$ 的邻居更有可能是真正的正样本。因此，重新基于原始距离计算权重并为更近的样本赋予较大的权重是令人信服和合理的。
3. 仅仅考虑上下文信息在测量两个人的相似性时会带来相当大的障碍，因为不可避免的变化使得难以区分足够的上下文信息。因此，将原始距离和Jaccard距离结合起来对于一个稳健的距离是很重要的。

受(2)的启发，提出了k-互惠特征来解决前两个缺点，通过将k-互惠近邻集编码为向量 $\mathbf{V}_p = [\mathcal{V}_{p, g_1}, \mathcal{V}_{p, g_2}, \ldots, \mathcal{V}_{p, g_N}]$，其中 $\mathcal{V}_{p, g_i}$ 最初由一个二进制指示函数定义如下：

$$\mathcal{V}_{p, g_i} = \begin{cases} 1 & \text{如果 } g_i \in \mathcal{R}^*(p, k) \\ 0 & \text{否则} \end{cases}$$

通过这种方式，k-互惠邻居集可以表示为一个N维向量，其中向量的每个项表示对应的图像是否包含在$\mathcal{R}^*(p, k)$中。然而，这个函数仍然将每个邻居视为等同的。直观上，离探测者 $p$ 更近的邻居应该与探测者 $p$ 更相似。因此，我们根据探测者与其邻居之间的原始距离重新分配权重，我们通过成对距离的高斯核重新定义公式如下：

$$\mathcal{V}_{p, g_i} = \begin{cases} e^{-d(p,g_i)} & \text{如果 } g_i \in \mathcal{R}^*(p, k) \\ 0 & \text{否则} \end{cases}$$

通过这种方式，硬权重（0或1）被转换为软权重，离探测者更近的邻居被分配更大的权重，而更远的邻居则分配较小的权重。基于上述定义，交集和并集中候选项的数量可以计算为：

$$|\mathcal{R}^*(p, k) \cap \mathcal{R}^*(g_i, k)| = \|\min(\mathbf{V}_p, \mathbf{V}_{g_i})\|_1$$

$$|\mathcal{R}^*(p, k) \cup \mathcal{R}^*(g_i, k)| = \|\max(\mathbf{V}_p, \mathbf{V}_{g_i})\|_1$$

其中，$\min$ 和 $\max$ 操作基于元素的最小化和最大化，$\|\cdot\|_1$ 是 $L_1$ 范数。因此，我们可以将公式5中的Jaccard距离重新写为：

$$d_J(p, g_i) = 1 - \frac{\sum_{j=1}^{N} \min(\mathcal{V}_{p, g_j}, \mathcal{V}_{g_i, g_j})}{\sum_{j=1}^{N} \max(\mathcal{V}_{p, g_j}, \mathcal{V}_{g_i, g_j})}$$

通过将公式5转换为公式10，我们成功地将集合比较问题转换为纯向量计算，这在实际操作中要容易得多。

Local Query Expansion

模仿同一类图像可能共享相似特征的想法，我们使用探测者 (p) 的k-近邻来实现局部查询扩展。局部查询扩展定义为：

$$\mathbf{V}_p = \frac{1}{|N(p, k)|} \sum_{g_i \in N(p, k)} \mathbf{V}_{g_i}$$

因此，k-互惠特征 $\mathbf{V}_p$ 被探测者 $p$ 的k-近邻扩展。请注意，我们在探测者 $p$ 和图库 $g_i$ 上都实现了此查询扩展。由于在k-近邻中会有噪声，我们将局部查询扩展中使用的 $N(p, k)$ 的大小限制为较小的值。为了区分公式7和公式11中使用的 $\mathcal{R}^*(g_i, k)$ 和 $N(p, k)$ 的大小，我们将前者记为 $k_1$，后者记为 $k_2$，其中 $k_1 > k_2$。

Final Distance

在本小节中，我们关注公式5的第三个缺点。虽然大多数现有的重新排名方法在重新排名时忽略了原始距离的重要性，但我们将原始距离和Jaccard距离联合起来，修正初始排名列表。最终距离 $d^*$ 定义为：

$$d^*(p, g_i) = (1 - \lambda)d_J(p, g_i) + \lambda d(p, g_i)$$

其中 $\lambda \in [0, 1]$ 表示惩罚因子，它惩罚离探测者 $p$ 较远的图库。当 $\lambda = 0$ 时，只考虑k-互惠距离。相反，当 $\lambda = 1$ 时，只考虑原始距离。第4节讨论了 $\lambda$ 的影响。最后，通过对最终距离进行升序排序，可以得到修正后的排名列表 $\mathcal{L}^*(p, \mathcal{G})$。

Complexity Analysis

在所提出的方法中，大部分计算成本集中在所有图库对的成对距离计算上。假设图库集合的大小为 $N$，距离度量和排名过程所需的计算复杂度分别是 $O(N^2)$ 和 $O(N^2 \log N)$。然而，在实际应用中，我们可以离线预先计算成对距离并获取图库的排名列表。因此，给定一个新的探测者 $p$，我们只需计算 $p$ 与图库之间的成对距离，计算复杂度为 $O(N)$，并对所有最终距离进行排序，计算复杂度为 $O(N \log N)$。

实验结果

主要将所提方法在两个基于图片的数据集，一个基于视频的数据集以及一个端到端的数据集上进行了实验，所提方法相比基线，效果均有明显的提升。

参数分析

k1的影响

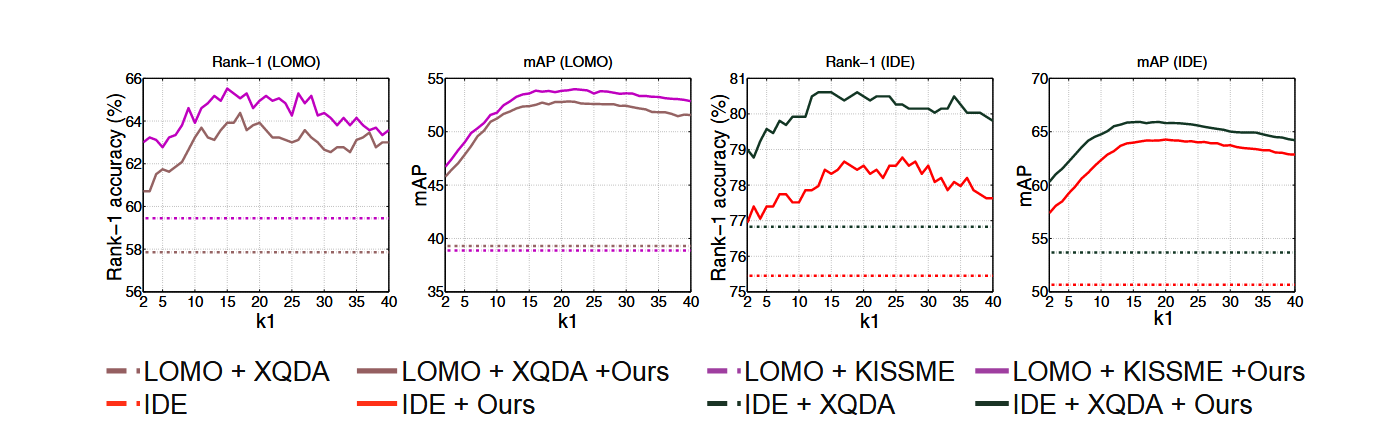
随着$k_1$的上升，rank-1准确率先上升，在$k_1=20$时达到最高，然后缓慢下降。这是因为开始的时候$k$较小，随着$k$越来越大，k-互惠特征中错误的邻居数量逐渐增多，导致性能下降。

k2的影响

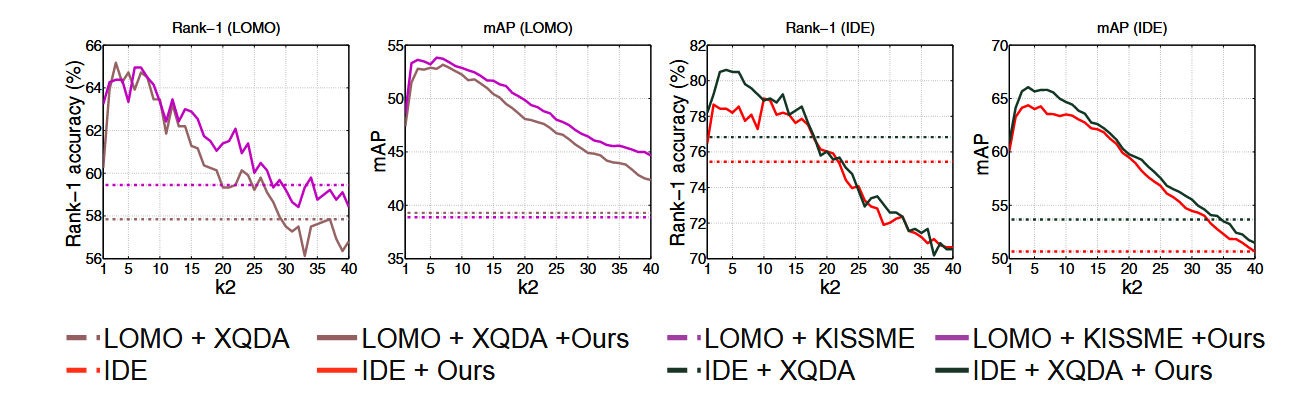
$k_2$的影响如上图所示。当$k_2$等于1时，不考虑本地查询扩展。显然，随着$k_2$在合理范围内增加，性能也会提高。请注意，为 $k_2$ 分配太大的值会降低性能。因为它可能会导致本地查询扩展中以指数方式包含错误匹配，这无疑会损害该功能，从而损害性能。事实上，当给$k_2$设置合适的值时，本地查询扩展对于进一步提升性能是非常有好处的。

λ的影响

参数 $\lambda$ 的影响如上图所示。注意，当 $\lambda$ 设置为 0 时，我们只考虑 Jaccard 距离作为最终距离；相反，当 $\lambda$ 等于1时，忽略了杰卡德距离，其结果正是使用纯原始距离得到的基线结果。可以看出，当仅考虑杰卡德距离时，我们的方法始终优于基线。这表明所提出的杰卡德距离对于重新排序是有效的。此外，当同时考虑原始距离和Jaccard距离时，当 $\lambda$ 值在0.3左右时，性能得到进一步提高，这表明原始距离对于重新排序也很重要。

总结

在这篇论文中，我们解决了行人再识别（re-ID）中的重排序问题。我们提出了一种k-互惠特征，通过将k-互惠最近邻居编码成一个单一向量，使得重排序过程可以通过向量比较轻松地完成。为了从相似样本中捕捉相似性关系，提出了局部扩展查询以获得更稳健的k-互惠特征。基于原始距离和Jaccard距离的组合计算的最终距离在多个大规模数据集上有效地提升了re-ID的性能。值得一提的是，我们的方法是完全自动化且无监督的，并且可以轻松地应用于任何排名结果。