学习整理自:diffusion model(二):DDIM技术小结 (denoising diffusion implicit model) | 莫叶何竹🍀 (myhz0606.com),欢迎阅读原文
文章基本信息
- 文章名称:Denoising Diffusion Implicit Models
- 发表会议/年份:ICLR 2021
- 作者:Jiaming Song, Chenlin Meng & Stefano Ermon
- 单位:Stanford University
背景
尽管去噪扩散概率模型(DDPM)无需对抗训练即可实现高质量图像生成,但其采样过程依赖于马尔可夫假设,需要较多的时间步才能得到较好的生成效果。本文介绍的去噪扩散隐式模型(DDIM)是一种更有效的迭代隐式概率模型,训练过程与DDPM相同,但采样过程比DDPM快10到50倍。
DDPM为何慢
从DDPM中我们知道,其扩散过程(前向过程,或加噪过程,forward process)被定义为一个马尔可夫过程:
q(x1:T∣x0):=t=1∏Tq(xt∣xt−1),
其中:
q(xt∣xt−1)=N(xt;αtxt−1,(1−αt)I)
通过这样设置,前向过程有一个很好的性质,可以通过 x0 得到任意时刻 xt 的分布,而无需繁琐的链式计算:
q(xt∣x0):=∫q(x1:t∣x0)dx1:(t−1)=N(xt;αtˉx0,(1−αtˉ)I)(1)
其去噪过程(也有叫逆向过程,reverse process)也是一个马尔可夫过程:
pθ(x0:T)=p(xT)t=1∏Tpθ(xt−1∣xt),
其中:
p(xT):=N(0,I),
并且:
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),σtI)
从式 (1) 可以看出,当 t 足够大时, q(xt∣x0) 对所有 x0 都收敛于标准高斯分布。因此DDPM在去噪过程中定义:
pθ(xT):=N(0,I)
并且采用一个较大的采样时间步数 T。在对 pθ(xt−1∣xt) 的推导中,DDPM用到了一阶马尔可夫假设,使得 p(xt∣xt−1,x0)=p(xt∣xt−1),因此重建的步长非常长,导致速度慢。
DDIM推理
DDPM速度慢的本质原因是对马尔可夫假设的依赖,导致重建需要较多的步长。那么不用一阶马尔可夫假设,有没有另一种方法推导出采样分布p(xt−1∣xt,x0)呢?
DDIM所提出的初衷就是:
- 维持DDPM前向推理过程中的马尔可夫假设(可以直接使用DDPM中所训练的噪声预测模型)
- 改变DDPM反向推理中的马尔可夫假设让采样分布的推导不依赖马尔可夫假设(这样不需要一步一步推回去)
DDIM采样分布求解
回到我们的目标,如何推出式子左边:
p(xt−1∣xt,x0)=p(xt∣x0)p(xt∣xt−1,x0)⋅p(xt−1∣x0)
但是这里右边式子中p(xt∣xt−1,x0)我们是不知道的,为了求解式子左边,在DDPM中我们是根据一阶马尔可夫假设假设了p(xt∣xt−1,x0)=p(xt∣xt−1)。从而推出左边p(xt−1∣xt,x0)为正态分布,然后得出答案。
根据DDPM的结果参考,采样分布p(xt−1∣xt,x0)是一个高斯分布,且均值是x0,xt的线性函数。
在DDIM中,为了不依赖p(xt∣xt−1,x0)(马尔可夫假设),作者做出了更为大胆的假设,作者假设p(xt−1∣xt,x0)为任意正态分布,只需要满足下述等式即可:
p(xt−1∣xt,x0)=N(xt−1;λx0+kxt,σt2I)
该采样分布有3个自由变量λ,k,σt,但是DDIM要维持与DDPM一致的正向推理分布:q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I) 。
根据数学归纳法,只需要保证q(xt−1∣x0)=N(xt−1;αˉt−1x0,(1−αˉt−1)I).
所以最终问题变为了,已知q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I),请寻找p(xt−1∣xt,x0)=N(xt−1;λx0+kxt,σt2I)的一组解λ∗,k∗,σt∗,使得q(xt−1∣x0)=N(xt−1;αˉt−1x0,(1−αˉt−1)I)。
即使得下式成立:
∫xtp(xt−1∣xt,x0)q(xt∣x0)dxt=q(xt−1∣x0)
可以使用待定系数法进行求解
首先对xt−1和ϵt−1′进行采样得:xt−1=λx0+kxt+σtϵt−1′ϵt−1′∼N(0,I)
根据q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I),可采样xt,ϵt′∼N(0,I):
xt=αˉtx0+1−αˉtϵt′
我们直接带入:
xt−1=λx0+k(αˉtx0+1−αˉtϵt′)+σtϵt−1′
合并同类项得到:
xt−1=(λ+kαˉt)x0+(k2(1−αˉt)+σt2)ϵˉt−1ϵˉt−1∼N(0,I)
根据q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I),可采样xt−1,ϵt−1∼N(0,I):
xt−1=αˉt−1x0+1−αˉt−1ϵt−1
结合上面两个式子,不难得到:
{λ+kαˉt=αˉt−1k2(1−αˉt)+σt2=1−αˉt−1
然后解得:
k∗=1−αˉt1−αˉt−1−σt2
λ∗=αˉt−1−1−αˉt−1−σt21−αˉtαˉt
σt∗=σ
综上将上面三个参数k∗,λ∗,σt∗带入我们可以得到:
p(xt−1∣xt,x0)=N(xt−1;αˉt−1x0+1−αˉt−1−σt21−αˉtxt−αˉtx0,σt2I)
综上,说明可以找到一组解满足题述条件。其中,不同的σt对应不同的生成过程。由于前向过程没变,故可以直接用DDPM训练的噪声预测模型。采样过程如下:
xt−1=αˉt−1x0+1−αˉt−1−σt2(1−αˉtxt−αˉtx0)+σtϵ
然后同DDPM,我们将x0用xt和ϵθ替代。
x0=αˉt1(xt−1−αˉtϵθ(xt,t))
最终化简得:
xt−1=αˉt−1αˉtxt−1−αˉtϵθ(xt,t)+1−αˉt−1−σt2ϵθ(xt,t)+σtϵ
其中只有σt是未知的,需要注意以下两个σt的特殊取值:
- 当σt=(1−αˉt−1)/(1−αˉt)1−αˉt/αˉt−1,此时的生成过程与DDPM一致
- 当σt为0时,此时采样过程中添加的随机噪声项为0,采样过程是确定的,就是作者所提出的DDIM,此时的递推公式为:
xt−1=αˉt−1αˉtxt−1−αˉtϵθ(xt,t)+1−αˉt−1ϵθ(xt,t)
DDIM如何加速采样
上面我们已经推导了DDIM如何从状态t推导到状态t−1,但是由于DDIM的反向过程没有受到马尔可夫的限制,因此他其实是可以从状态t直接推到前面任意一个状态的,从状态t推导到前面的状态t−m(m<t)可以表示为如下式子:
xt−m=αˉt−mαˉtxt−1−αˉtϵθ(xt,t)+1−αˉt−mϵθ(xt,t)
一般加速就是将原先是一步一步预测变成n步n步进行预测。
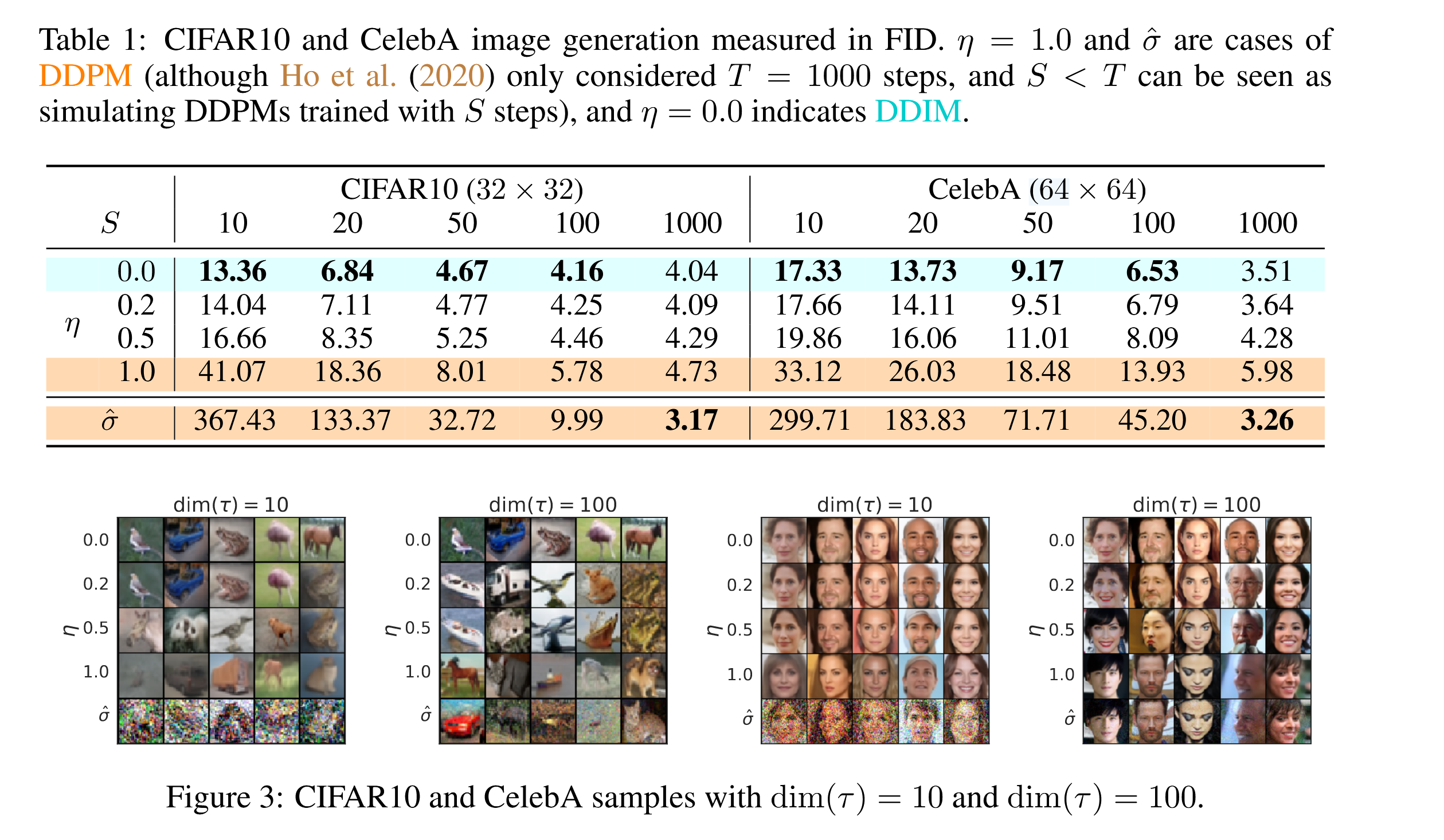
论文中也展示了使用不同的n所带来的结果,可以看到DDIM在较小采样步长时就能达到较好的生成效果。如CIFAR10 S=50就达到了S=1000的90%的效果,与之相对DDPM只能达到10%左右的FID效果。

其中,dim(L)表示的是采样序列的长度
DDIM区别于DDPM两个重要的特性
采样一致性
我们知道DDIM将σt设置为0,这让采样过程是确定的,只受xT影响。作者发现,当给定xT,不同的的采样时间序列τ所生成图片都很相近,xT似乎可以视作生成图片的隐编码信息。
有个小trick,我们在实际的生成中可以先设置较小的采样步长(迭代次数)进行生成,若生成的图片是我们想要的,则用较大的步长重新生成高质量的图片。
语义插值效应(sementic interpolation effect)
即然xT可能是生成图片的隐空间编码,那么它是否具备其它隐概率模型(如GAN2,VAE)所观察到的语义插值效应呢?
首先从高斯分布采样两个随机变量xT(0),xT(1),并用他们做图像生成得到下图最左侧与最右侧的结果。随后用球面线性插值方法(spherical linear interpolation,Slerp)对xT(1),xT(2)他们进行插值,得到一系列中间结果:
xT(α)=sin(θ)sin((1−α)θ)xT(0)+sin(θ)sin(αθ)xT(1)
其中θ=arccos(∥xT(0)∥∥xT(1)∥(xT(0))TxT(1)) ,结果如下所示,可以明确看出来还是有一定语义插值效应的。