2023-12-01
题目传送门:2661. 找出叠涂元素 - 力扣(LeetCode)
本题主要就是一个哈希表的思想,先使用一个map数据结构将每个元素和他的二维位置对应起来,这样可以实现O(1)查询,然后设置两个数组大小为每行每列,记录当前行列还剩的没染色的格子的数量,然后遍历arr中的每个元素,更新元素对应行列剩余未染色格子的个数。当发现当前元素对应行列有一个未染色格子剩余量为0时,输出即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : int firstCompleteIndex (vector<int >& arr, vector<vector<int >>& mat) int m = mat.size (), n =mat[0 ].size (); vector<int > row (m,n) ; vector<int > col (n,m) ; map<int ,pair<int ,int >> mp; for (int i=0 ;i<m;++i){ for (int j=0 ;j<n;++j){ mp[mat[i][j]] = pair <int , int >(i,j); } } for (int i=0 ;i<m*n;++i){ int x = mp[arr[i]].first, y = mp[arr[i]].second; row[x]--; col[y]--; if (row[x]==0 ||col[y]==0 ) return i; } return m*n-1 ; } };
2023-12-02
题目传送门:1094. 拼车 - 力扣(LeetCode)
一道非常经典的差分数组题,先对上下车站点进行排序,然后维护一个以站点为索引的差分数组,前缀和代表车到达当前站点时,车上的乘客数,乘客数大于capacity即不行,否则就可以。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution {public : bool carPooling (vector<vector<int >>& trips, int capacity) vector<int > pass_now (1001 ,0 ) ; sort (trips.begin (),trips.end (),[](vector<int > &a,vector<int > &b){ if (a[1 ] == b[1 ])return a[2 ]<b[2 ]; else return a[1 ]<b[1 ]; }); int max_dis = 0 ; for (auto &trip:trips){ pass_now[trip[1 ]] += trip[0 ]; pass_now[trip[2 ]] -= trip[0 ]; max_dis = max (max_dis,trip[2 ]); } int now = 0 ; for (int i=0 ;i<=max_dis;i++){ now += pass_now[i]; if (now>capacity)return false ; } return true ; } };
2023-12-03
题目传送门:1423. 可获得的最大点数 - 力扣(LeetCode)
脑筋急转弯题目,既然要让我们求两边取的最大,那么就是让我们反过来取中间的最小。这样就从取不连续的数变成取连续的了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : int maxScore (vector<int >& cardPoints, int k) int sum_point = 0 ,n = cardPoints.size (); for (auto &cardPoint:cardPoints)sum_point+=cardPoint; int res = n-k; int minn,capa=0 ,now=0 ; for (int i=0 ;i<n;++i){ if (capa<res) now += cardPoints[i], capa += 1 ; else { if (i == res) minn = now; now = now - cardPoints[i-res] + cardPoints[i]; minn = min (minn,now); } } return sum_point - minn; } };
2023-12-04
题目传送门:1038. 从二叉搜索树到更大和树 - 力扣(LeetCode)
今天的题还是有点意思,借机学习一下C++指针版本的二叉树如何书写, 题目要求我们将每个节点的值替换为值大于等于当前节点值的和,那么这个时候我们可以稍微思考一下二叉树的性质,不难发现,我们进行反向中序遍历时,生成的遍历序列就是从大到小的一个排序。那么我们按照这个顺序更新每一个节点即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution {public : int sumnow = 0 ; TreeNode* bstToGst (TreeNode* root) { if (root!=nullptr ) { if (root->right!=nullptr ) bstToGst (root->right); sumnow += root->val; root->val = sumnow; if (root->left!=nullptr ) bstToGst (root->left); } return root; } };
2023-12-05
题目传送门:2477. 到达首都的最少油耗 - 力扣(LeetCode)
今天的题目还是有点意思,感觉是之前一个周赛没做出来的题目,因为题目中还是有一些细节需要注意,这里就稍微梳理一下。
首先学习了C++内嵌函数的写法。
模板写法大概如下所示:
1 function<int (int , int )> dfs = [&](int u,int fa) -> int {
上面的代码,定义了一个名为 dfs 的函数,它接受两个整数参数 u 和 fa,返回一个整数值。这个函数是一个匿名函数(即没有名称的函数),它是一个模板函数,模板参数 int(int, int) 表示该函数接受两个整数参数并返回一个整数值。
代码中的 -> 符号表示函数的返回类型,它位于函数定义的末尾。int(int, int) 是函数的参数类型,int 表示返回值类型,int 和 int 分别表示两个参数的类型。
[&](int u,int fa) -> int 表示这是一个左值引用捕获的匿名函数,它捕获了函数外部的变量 u 和 fa 的引用。这使得在函数内部可以修改这些变量的值,而不会影响到函数外的变量。
总之,这段代码定义了一个名为 dfs 的匿名函数,它接受两个整数参数 u 和 fa,返回一个整数值。记住以后都这么写就对啦。 (还有需要注意的就是,最后}后需要加;)
接下来就是本题的一些解题感想了,因为是树形结构,所以不难想到会用递归这种算法,在本题中递归我们回溯的时候传递子树大小。同时我们定义一个变量用于存储最终的耗油量,
本题大致思路就是,对于当前节点在使用递归已知其子树大小后,再用耗油量变量加上当前节点指向其父亲节点那条边上的耗油量,该耗油量计算方式如下:
o i l = c e i l ( ( s i z e + 1 ) / s e a t s ) oil = ceil((size+1)/seats)
o i l = ce i l (( s i ze + 1 ) / se a t s )
其中size为当前节点子树大小,ceil是向上取整操作
最后代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public : long long minimumFuelCost (vector<vector<int >>& roads, int seats) vector<vector<int >> edge (roads.size ()+1 ); for (auto &road:roads) { int u = road[0 ],v = road[1 ]; edge[u].push_back (v); edge[v].push_back (u); } long long ans = 0 ; function<int (int , int )> dfs = [&](int u,int fa) -> int { if (edge[u].size ()==1 &&u!=0 ){ ans += 1 ; return 1 ; } int size = 0 ; for (auto &v:edge[u]){ if (v == fa) continue ; size += dfs (v,u); } if (u!=0 ) ans += (size) / seats + 1 ; return size+1 ; }; dfs (0 ,-1 ); return ans; } };
2023-12-06
题目传送门:2646. 最小化旅行的价格总和 - 力扣(LeetCode)
今天的题目还是有点有意思,一道树形DP记录一下。首先我们需要抓住一个要点就是,因为是在树上,所以路径是唯一的。所以解本题的第一步是统计走完所有的trip时,树上的每个节点被走过多少次。第一步就是一个简单的dfs搜索,当搜索到正确的路径后,回溯时将路径上每个节点经过的次数+1。
经过第一步后,我们就可以重新计算每个点的代价,就是用原来每个点的价格乘上次数。然后就进入一个标准的树形DP染色问题了。定义dp数组dp[i][j]其中i代表的是当前节点,j取值范围是0,1。0代表的是当前节点不优惠,1代表的是当前节点染色。状态转移方程如下所示:
d p [ u ] [ 0 ] = ( ∑ m i n ( d p [ v ] [ 0 ] , d p [ v ] [ 1 ] ) ) + c o s t [ u ] dp[u][0] = (\sum min(dp[v][0],dp[v][1]))+ cost[u]
d p [ u ] [ 0 ] = ( ∑ min ( d p [ v ] [ 0 ] , d p [ v ] [ 1 ])) + cos t [ u ]
d p [ u ] [ 1 ] = ( ∑ d p [ v ] [ 0 ] ) + c o s t [ u ] / 2 dp[u][1] = (\sum dp[v][0]) + cost[u]/2
d p [ u ] [ 1 ] = ( ∑ d p [ v ] [ 0 ]) + cos t [ u ] /2
其中v是u的儿子
更新就是和传统树形DP一样是在进行递归后回溯的时候更新。
最终代码如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 class Solution {public : int minimumTotalPrice (int n, vector<vector<int >>& edges, vector<int >& price, vector<vector<int >>& trips) vector<int > nums (n+1 ,0 ) ; vector<vector<int >> edge (n+1 ); for (auto &tmp:edges){ int u = tmp[0 ], v = tmp[1 ]; edge[u].push_back (v); edge[v].push_back (u); } function<bool (int ,int ,int )> dfs = [&](int u,int fa,int tar) { if (u == tar){ nums[u]++; return true ; } for (auto &v:edge[u]){ if (v==fa) continue ; if (dfs (v,u,tar)) { nums[u]+=1 ; return true ; } } return false ; }; for (auto &trip:trips) { dfs (trip[0 ],-1 ,trip[1 ]); } vector<vector<int >> dp (n+1 ,vector <int >(2 ,0 )); function <void (int ,int )> dfs_dp = [&](int u,int fa) { dp[u][0 ] = price[u]*nums[u]; dp[u][1 ] = price[u]*nums[u]/2 ; for (auto &v:edge[u]){ if (v==fa) continue ; dfs_dp (v,u); dp[u][0 ] += min (dp[v][0 ],dp[v][1 ]); dp[u][1 ] += dp[v][0 ]; } }; dfs_dp (0 ,-1 ); return min (dp[0 ][0 ],dp[0 ][1 ]); } };
2023-12-07
题目传送门:1466. 重新规划路线 - 力扣(LeetCode)
此题就是一个非常简单的树的遍历题目,我们只需要判断遍历过程中,边的方向,然后决定是否要反转即可。
注意
本题中pair相关的写法,压入vector的时候使用的是{},for循环提取出来的时候使用的是[]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : int minReorder (int n, vector<vector<int >>& connections) vector<vector<pair<int ,int >>> edge (n+1 ); for (auto &c:connections){ int a = c[0 ], b = c[1 ]; edge[a].push_back ({b,1 }); edge[b].push_back ({a,0 }); } int ans = 0 ; function<void (int ,int )> dfs = [&](int u,int fa){ for (auto &[v,type]:edge[u]){ if (v==fa) continue ; ans += type; dfs (v,u); } }; dfs (0 ,-1 ); return ans; } };
2023-12-08
题目传送门:2008. 出租车的最大盈利 - 力扣(LeetCode)
今天的这道题首先读完题目后就可以猜出应该是一道DP题,然后我们在观察数据规模,行程数量最大为3e4,站点取值范围为1e5。所以我们设计的DP算法的时间复杂度只能是O ( n ) O(n) O ( n ) O ( n l o g n ) O(nlogn) O ( n l o g n )
方法一:动态规划+二分查找
因为这道题对顺序有一些要求,所以不难想到可能会使用排序或者二分这类算法。
当然我们还是先设计dp状态转移方程,方程如下所示:
d p [ i ] = m a x ( d p [ i − 1 ] , d p [ j ] + v a l [ i ] ) dp[i] = max(dp[i-1],dp[j]+val[i])
d p [ i ] = ma x ( d p [ i − 1 ] , d p [ j ] + v a l [ i ])
其中索引号代表的是每个人的编号(重新排序过的,依终点大小从小到大进行排序),v a l [ i ] val[i] v a l [ i ]
j j j i i i j j j
因此这道题就比较好解决了:
先按照终点从小到大排序
遍历所有的人,遵循上面的转移方程进行状态转移
转移的过程中,进行二分寻找j
最终代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : long long maxTaxiEarnings (int n, vector<vector<int >>& rides) sort (rides.begin (),rides.end (), [](const vector<int > &a, const vector<int > &b){ if (a[1 ]==b[1 ])return a[0 ] < b[0 ]; return a[1 ] < b[1 ]; }); int p_num = rides.size (); vector<long long > dp (p_num+1 ) ; for (int i=0 ;i<p_num;++i){ int j = upper_bound (rides.begin (), rides.begin () + i, rides[i][0 ], [](int x, const vector<int > &r){ return x < r[1 ]; }) - rides.begin (); dp[i+1 ] = max (dp[i], dp[j]+rides[i][1 ]-rides[i][0 ]+rides[i][2 ]); } return dp[p_num]; } };
方法二:动态规划+哈希表
方法一可能存在不直观(dp数组索引是人)以及算法时间复杂度稍高的问题。我们其实使用动态规划结合哈希表的方法可以将算法时间复杂度优化到O ( n ) O(n) O ( n )
我们使用一个哈希表rideMap[end],记录终点为end的所有乘客信息,不同于之前的方法这里dp[i]代表到达第i i i dp[0]=0。对于每个地点i有两种可能的转移:
i i i d p [ i ] = d p [ i − 1 ] dp[i]=dp[i-1] d p [ i ] = d p [ i − 1 ] 有人下车,最大利润为d p [ i ] = m a x ( d p [ s t a r t j ] + e n d [ j ] − s t a r t [ j ] + t i p [ j ] ) dp[i]=max(dp[start_j]+end[j]-start[j]+tip[j]) d p [ i ] = ma x ( d p [ s t a r t j ] + e n d [ j ] − s t a r t [ j ] + t i p [ j ])
理解完整个过程最终的代码就是:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : long long maxTaxiEarnings (int n, vector<vector<int >>& rides) vector<long long > dp (n+1 ) ; unordered_map<int , vector<vector<int >>> rideMap; for (const auto &ride: rides) { rideMap[ride[1 ]].push_back (ride); } for (int i = 1 ; i <= n; ++i){ dp[i] = dp[i-1 ]; for (const auto &ride : rideMap[i]) { dp[i] = max (dp[i], dp[ride[0 ]] + ride[1 ] - ride[0 ] + ride[2 ]); } } return dp[n]; } };
2023-12-09
题目传送门:2048. 下一个更大的数值平衡数 - 力扣(LeetCode)
这个题打一个表,用一个可爱的二分就可以解决,(二分直接调用upper_bound函数)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution {public : const vector<int > balance { 1 , 22 , 122 , 212 , 221 , 333 , 1333 , 3133 , 3313 , 3331 , 4444 , 14444 , 22333 , 23233 , 23323 , 23332 , 32233 , 32323 , 32332 , 33223 , 33232 , 33322 , 41444 , 44144 , 44414 , 44441 , 55555 , 122333 , 123233 , 123323 , 123332 , 132233 , 132323 , 132332 , 133223 , 133232 , 133322 , 155555 , 212333 , 213233 , 213323 , 213332 , 221333 , 223133 , 223313 , 223331 , 224444 , 231233 , 231323 , 231332 , 232133 , 232313 , 232331 , 233123 , 233132 , 233213 , 233231 , 233312 , 233321 , 242444 , 244244 , 244424 , 244442 , 312233 , 312323 , 312332 , 313223 , 313232 , 313322 , 321233 , 321323 , 321332 , 322133 , 322313 , 322331 , 323123 , 323132 , 323213 , 323231 , 323312 , 323321 , 331223 , 331232 , 331322 , 332123 , 332132 , 332213 , 332231 , 332312 , 332321 , 333122 , 333212 , 333221 , 422444 , 424244 , 424424 , 424442 , 442244 , 442424 , 442442 , 444224 , 444242 , 444422 , 515555 , 551555 , 555155 , 555515 , 555551 , 666666 , 1224444 }; int nextBeautifulNumber (int n) return *upper_bound (balance.begin (), balance.end (), n); } };
2023-12-10
题目传送门:70. 爬楼梯 - 力扣(LeetCode)
刚好和动态规划(基础版)第一题一样,直接抄过来即可。
记忆化搜索版:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : int climbStairs (int n) vector<int > dp (n+1 ,-1 ) ; dp[0 ] = 1 ;dp[1 ] = 1 ; function<int (int )> dfs = [&](int now){ if (dp[now]!=-1 ) return dp[now]; dp[now-1 ] = dfs (now-1 ); dp[now-2 ] = dfs (now-2 ); return dp[now-1 ] + dp[now-2 ]; }; return dfs (n); } };
递推版:
1 2 3 4 5 6 7 8 9 10 11 class Solution {public : int climbStairs (int n) vector<int > dp (n+1 ,0 ) ; dp[0 ] = 1 ;dp[1 ] = 1 ; for (int i=2 ;i<=n;++i){ dp[i] = dp[i-1 ]+dp[i-2 ]; } return dp[n]; } };
2023-12-11
题目传送门:1631. 最小体力消耗路径 - 力扣(LeetCode)
这道题注意题目不要读错,其实就是一道最短路板子题,正好借助这个机会熟悉一下Dijkstra的C++写法。
最终代码如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 struct DIS { int x, y, val; DIS (int _x,int _y, int _val): x (_x), y (_y), val (_val) {} bool operator < (const DIS& that) const { return that.val < val; } }; class Solution {public : int minimumEffortPath (vector<vector<int >>& heights) int m = heights.size (), n = heights[0 ].size (); vector<vector<bool >> vis (m,vector <bool >(n, false )); vector<vector<int >> dis (m, vector <int >(n, INT_MAX)); priority_queue<DIS> q; dis[0 ][0 ] = 0 ; q.emplace (0 ,0 ,0 ); vector<vector<int >> dirs = {{0 ,1 },{1 ,0 },{-1 ,0 },{0 ,-1 }}; while (!q.empty ()){ auto [x,y,val] = q.top ();q.pop (); if (vis[x][y]) continue ; vis[x][y] = true ; for (auto &dir:dirs){ int nx = x + dir[0 ], ny = y + dir[1 ]; if (nx>=0 && nx<m && ny>=0 && ny<n && dis[nx][ny] > max (dis[x][y],abs (heights[x][y]-heights[nx][ny]))){ dis[nx][ny] = max (dis[x][y],abs (heights[x][y]-heights[nx][ny])); q.emplace (nx,ny,dis[nx][ny]); } } } return dis[m-1 ][n-1 ]; } };
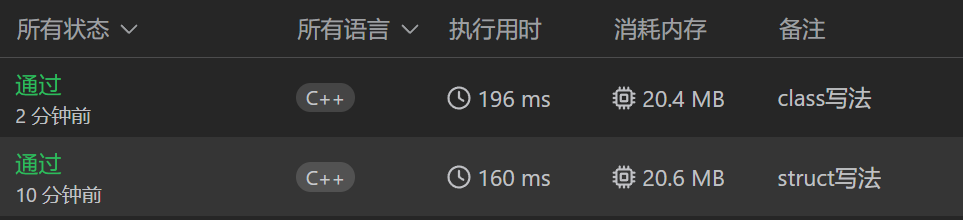
上述代码使用了struct这就不是很正统C++,所以我们当然也可以写成类的形式:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class DIS {public : int x, y, val; DIS (int _x, int _y, int _val) : x (_x), y (_y), val (_val) {} bool operator < (const DIS& that) const { return that.val < val; } }; class Solution {public : int minimumEffortPath (vector<vector<int >>& heights) int m = heights.size (), n = heights[0 ].size (); vector<vector<bool >> vis (m,vector <bool >(n, false )); vector<vector<int >> dis (m, vector <int >(n, INT_MAX)); priority_queue<DIS> q; dis[0 ][0 ] = 0 ; q.emplace (0 ,0 ,0 ); vector<vector<int >> dirs = {{0 ,1 },{1 ,0 },{-1 ,0 },{0 ,-1 }}; while (!q.empty ()){ auto [x,y,val] = q.top ();q.pop (); if (vis[x][y]) continue ; vis[x][y] = true ; for (auto &dir:dirs){ int nx = x + dir[0 ], ny = y + dir[1 ]; if (nx>=0 && nx<m && ny>=0 && ny<n && dis[nx][ny] > max (dis[x][y],abs (heights[x][y]-heights[nx][ny]))){ dis[nx][ny] = max (dis[x][y],abs (heights[x][y]-heights[nx][ny])); q.emplace (nx,ny,dis[nx][ny]); } } } return dis[m-1 ][n-1 ]; } };
当然不出意外, 还是struct的效率会高一些,也建议以后都写成struct,在里面重定义小于运算符。
其他注意事项
auto取top中的结构体值
1 auto [x,y,val] = q.top ();q.pop ();
重定义运算符两个const都不能省略
1 2 3 bool operator < (const DIS& that) const { return that.val < val; }
int类型的最大值可以直接写INT_MAX
2023-12-12※
题目传送门:2454. 下一个更大元素 IV - 力扣(LeetCode)
此题需要用到单调栈的相关内容,单调栈基础详情见专项训练单调栈模块。
以下内容摘自灵神题解:
首先回想一下,怎么找下一个更大元素,即右侧最近的更大元素。
使用视频中讲的第二种做法,从左到右遍历数组,用一个(递减)单调栈s s s x x x x x x
在这个做法中,栈顶元素弹出后,就没有用了。但对于本题,我们需要的正是弹出去的元素!
再用一个(递减)单调栈 t t t s s s y y y t t t y y y
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution {public : vector<int > secondGreaterElement (vector<int >& nums) { int n = nums.size (); vector<int > ans (n, -1 ) , s, t ; for (int i = 0 ; i < n; ++i) { int x = nums[i]; while (!t.empty () && nums[t.back ()] < x){ ans[t.back ()] = x; t.pop_back (); } int j = s.size (); while (j && nums[s[j-1 ]] < x) j--; t.insert (t.end (), s.begin () + j, s.end ()); s.resize (j); s.push_back (i); } return ans; } };
2023-12-13
题目传送门:2697. 字典序最小回文串 - 力扣(LeetCode)
双指针签到题目,两个指针分别指向字符串头尾,标记的是回文串相对应的位置,遍历的过程中,left每向右移动一个位置,right就向左移动一个位置,这样会出现两种情况。
如果指向的字符一样,不做任何操作
如果指向的字母不同,将他们都变成这两个子母中较小的那个字母即可。
最后返回新的字符串。
最终代码如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : string makeSmallestPalindrome (string s) { int n = s.length (); for (int i=0 ;i<n/2 ;++i){ if (s[i]!=s[n-1 -i]){ if (s[i] < s[n-1 -i]) s[n-1 -i] =s[i]; else s[i] = s[n-1 -i]; } } return s; } };
2023-12-14
今天的这道题非常的有意思,读完题目后,大概就会有一个基本思路,就是能放上邮票的地方我们尽量放上邮票,最后我们看整个矩阵有没有空白的地方。
借用灵神 的思路概括一下:
由于邮票可以互相重叠,贪心地想,能放邮票就放邮票。
遍历所有能放邮票的位置去放邮票。注意邮票不能覆盖被占据的格子,也不能出界。
放邮票的同时,记录每个空格子被多少张邮票覆盖。如果存在一个空格子没被邮票覆盖,则返回 false,否则返回 true。
其实把上面的大体思路想明白了,根据之前的做题经验,这道题使用差分也比较明显了,就是还有一些细节需要注意一下。
因为要使用差分,所以我们放邮票从右下角开始放,这样好使用差分O ( 1 ) O(1) O ( 1 )
放邮票我们也是采用一个差分矩阵来记录,最后求二维前缀和就可以还原最终的邮票放置方法。
注意:以后写这种差分的题目,下标代表的都是从1开始,因为必须要留一个0保证求前缀和这类操作的统一性。
最终代码如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution {public : bool possibleToStamp (vector<vector<int >>& grid, int stampHeight, int stampWidth) int n = grid.size (), m = grid[0 ].size (); vector<vector<int >> s (n+1 ,vector <int >(m+1 ,0 )); for (int i=0 ; i<n; ++i) { for (int j=0 ; j<m; ++j){ s[i+1 ][j+1 ] = grid[i][j] + s[i][j+1 ] + s[i+1 ][j] - s[i][j]; } } vector<vector<int >> cov (n+2 ,vector <int >(m+2 ,0 )); for (int i=stampHeight; i<=n; ++i) { for (int j=stampWidth; j<=m; ++j){ int i1 = i - stampHeight + 1 ; int j1 = j - stampWidth + 1 ; if (s[i][j] - s[i][j1-1 ] - s[i1-1 ][j] + s[i1-1 ][j1-1 ] == 0 ){ cov[i1][j1] ++; cov[i+1 ][j1] -- ; cov[i1][j+1 ] --; cov[i+1 ][j+1 ] ++; } } } for (int i=1 ;i<=n;++i){ for (int j=1 ;j<=m;++j){ cov[i][j] += cov[i-1 ][j] + cov[i][j-1 ] - cov[i-1 ][j-1 ]; if (grid[i-1 ][j-1 ] == 0 && cov[i][j] == 0 ) return false ; } } return true ; } };
2023-12-15
题目传送门:2415. 反转二叉树的奇数层 - 力扣(LeetCode)
此题考察的是二叉树的层序遍历,其实就是一种bfs吧,通过本题可以更熟悉一下C++中指针和vector相关内容。
最终代码如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution {public : TreeNode* reverseOddLevels (TreeNode* root) { vector<vector<TreeNode*>> que (2 ); que[0 ].push_back (root); int now = 0 ; while (!que[now].empty ()){ for (auto node:que[now]){ if (node->left) que[1 -now].push_back (node->left); if (node->right) que[1 -now].push_back (node->right); } if (now) { int siz = que[now].size (); for (int i=0 ;i<siz/2 ;++i){ int tmp = que[now][i]->val; que[now][i]->val = que[now][siz-1 -i]->val; que[now][siz-1 -i]->val = tmp; } } while (!que[now].empty ()) que[now].pop_back (); now = 1 -now; } return root; } };
2023-12-16
题目传送门:2276. 统计区间中的整数数目 - 力扣(LeetCode)
还没太整明白:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 class Solution {public : vector<int > secondGreaterElement (vector<int >& nums) { int n = nums.size (); vector<int > ans (n, -1 ) , s, t ; for (int i = 0 ; i < n; ++i) { int x = nums[i]; while (!t.empty () && nums[t.back ()] < x){ ans[t.back ()] = x; t.pop_back (); } int j = s.size (); while (j && nums[s[j-1 ]] < x) j--; t.insert (t.end (), s.begin () + j, s.end ()); s.resize (j); s.push_back (i); } return ans; } };
2023-12-17
题目传送门:746. 使用最小花费爬楼梯 - 力扣(LeetCode)
一道非常基础的DP题目,这里就使用记忆化搜索解决了,需要注意的是cost最后压入一个0,来保证所有的操作一致性(代表已经到最高点了,往上走的开销为0)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : int minCostClimbingStairs (vector<int >& cost) int n = cost.size (); cost.emplace_back (0 ); vector<int > dp (n+1 , -1 ) ; dp[0 ] = cost[0 ]; dp[1 ] = cost[1 ]; function<int (int )> dfs = [&](int now){ if (dp[now]!=-1 ) return dp[now]; int a = dfs (now-1 ), b = dfs (now-2 ); dp[now] = cost[now] + min (a,b); return dp[now]; }; return dfs (n); } };
2023-12-18
题目传送门:162. 寻找峰值 - 力扣(LeetCode)
因为题目要求实现O ( log n ) O(\log n) O ( log n )
本题二分的思想其实很简单,我们需要明白一个道理,就是峰值一定是比较大的值,所以每次二分的时候判断当前mid位置与他左右位置数的大小关系,然后往大的地方更新区间即可。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : int findPeakElement (vector<int >& nums) int len = nums.size (); int l = 0 , r = len-1 ; function<long long (int )> getitem = [&](int i){ if (i<=-1 ||i>=len) return 2 *(long long )(INT_MIN); return (long long )(nums[i]); }; while (l <= r) { int mid = l + (r-l)/2 ; if (getitem (mid)>getitem (mid-1 )&&getitem (mid)>getitem (mid+1 )) return mid; if (getitem (mid)<getitem (mid+1 )) l = mid+1 ; else r = mid-1 ; } return -123123 ; } };
这里使用的是闭区间二分,需要注意的是0位置的左边以及len-1位置的右边定义的峰值大小都是2*INT_MIN,使用一个getitem函数来取值,其中需要考虑这种超出区间范围的问题。
其实上面的这种写法并不是很二分,可以再改进一下,如下所示(因为最后一定有峰顶,所以直接分为不可能为峰顶和可能为峰顶两类就可以判断出来谁是峰顶了):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : int findPeakElement (vector<int >& nums) int len = nums.size (); int l = 0 , r = len-1 ; function<long long (int )> getitem = [&](int i){ if (i<=-1 ||i>=len) return 2 *(long long )(INT_MIN); return (long long )(nums[i]); }; while (l <= r) { int mid = l + (r-l)/2 ; if (getitem (mid)<getitem (mid+1 )) l = mid+1 ; else r = mid-1 ; } return l; } };
可以仔细理解一下为啥把中间那个if注释掉。
最后返回l l l mid还是有可能是峰顶的,所以应该返回r + 1 r+1 r + 1 r + 1 = l r+1=l r + 1 = l l l l
2023-12-19
题目传送门:1901. 寻找峰值 II - 力扣(LeetCode)
同样也是二分,只不过是对每行的最大值进行二分,往mid前后行更大的最大值的地方更新区间。最终代码如下所示:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : int max_idx (vector<int > nums) return max_element (nums.begin (), nums.end ()) - nums.begin (); } vector<int > findPeakGrid (vector<vector<int >>& mat) { int n = mat.size (); int l = 0 , r = n-1 ; while (l<r){ int mid = l + (r-l)/2 ; int j = max_idx (mat[mid]); if (mat[mid][j] > mat[mid+1 ][j]) r = mid; else l = mid+1 ; } int ans = l; return vector<int >{ans,max_idx (mat[ans])}; } };
2023-12-20
题目传送门:2828. 判别首字母缩略词 - 力扣(LeetCode)
签到题,熟悉string的基本用法
1 2 3 4 5 6 7 8 9 10 class Solution {public : bool isAcronym (vector<string>& words, string s) if (words.size ()!=s.size ()) return false ; for (int i=0 ;i<words.size ();++i){ if (words[i][0 ]!=s[i]) return false ; } return true ; } };
2023-12-21
题目传送门:2866. 美丽塔 II - 力扣(LeetCode)
2023-12-22
题目传送门:1671. 得到山形数组的最少删除次数 - 力扣(LeetCode)
2023-12-23
题目传送门:1962. 移除石子使总数最小 - 力扣(LeetCode)
一道非常容易想的贪心题目,每次取最大减半即可。使用优先队列维护最大值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : int minStoneSum (vector<int >& piles, int k) priority_queue<int > pq; int sum_pile = 0 ; for (auto &pile:piles) { pq.emplace (pile); sum_pile += pile; } int ans = 0 ; for (int i=1 ;i<=k;++i){ int nw = pq.top (); ans += nw/2 ; pq.pop (); pq.emplace (nw-(nw/2 )); } return sum_pile - ans; } };
2023-12-24
题目传送门:1954. 收集足够苹果的最小花园周长 - 力扣(LeetCode)
一道非常明显的二分题目,将给定x苹果总数计算公式推出即可,使用左闭右开二分查找:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : long long minimumPerimeter (long long neededApples) function<long long (long long )> getApple = [&](long long x){ return (x*2 +1 )*x*(x+1 )*2 ; }; long long l = 0 , r = 100000 ; while (l<r) { long long mid = l + (r-l)/2 ; long long nwapple = getApple (mid); if (nwapple >= neededApples) r=mid; else l=mid+1 ; } return l*8 ; } };
2023-12-25
题目传送门:1276. 不浪费原料的汉堡制作方案 - 力扣(LeetCode)
再次复习一下二分闭区间写法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : vector<int > numOfBurgers (int tomatoSlices, int cheeseSlices) { function<bool (int )> search = [&](int x){ return x*4 +(cheeseSlices-x) * 2 >=tomatoSlices?true :false ; }; int l = 0 , r = cheeseSlices; while (l <= r){ int mid = l+(r-l)/2 ; if (search (mid)) r = mid-1 ; else l = mid+1 ; } return l*4 +(cheeseSlices-l)*2 == tomatoSlices?vector<int >{l,cheeseSlices-l}:vector<int >{}; } };
2023-12-26
题目传送门:1349. 参加考试的最大学生数 - 力扣(LeetCode)
2023-12-27
题目传送门:2660. 保龄球游戏的获胜者 - 力扣(LeetCode)
一道非常简单的签到题目:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : int isWinner (vector<int >& player1, vector<int >& player2) int n = player1.size (); int p1_sum = player1[0 ], p2_sum = player2[0 ]; for (int i=1 ;i<n;++i){ if (player1[i-1 ]==10 ) p1_sum += player1[i]*2 ; else if (i>1 &&player1[i-2 ]==10 ) p1_sum += player1[i]*2 ; else p1_sum += player1[i]; if (player2[i-1 ]==10 ) p2_sum += player2[i]*2 ; else if (i>1 &&player2[i-2 ]==10 ) p2_sum += player2[i]*2 ; else p2_sum += player2[i]; } return p1_sum == p2_sum?0 :p1_sum>p2_sum?1 :2 ; } };
2023-12-28
题目传送门:2735. 收集巧克力 - 力扣(LeetCode)
这道题题目描述有点歧义,需要结合样例理解题目意思,但是还是一道有点有意思的枚举。
理解清楚题意后我们不难发现,操作的次数是有限的,最多是等于种类数-1,然后我们观察数据范围<1000,因此我们可以采用枚举操作数的方式解决这道题目,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public : long long minCost (vector<int >& nums, int x) int len = nums.size (); vector<int >min_nw = nums; long long ans = 1000000000004 ; for (int i=0 ;i<len;++i){ long long tmp = (long long )i*x; for (int j=0 ;j<len;++j){ min_nw[j] = min (min_nw[j],nums[(j+i)%len]); tmp += min_nw[j]; } ans = min (ans,tmp); } return ans; } };
2023-12-29
题目传送门:2706. 购买两块巧克力 - 力扣(LeetCode)
签到题,代码如下:
1 2 3 4 5 6 7 8 class Solution {public : int buyChoco (vector<int >& prices, int money) sort (prices.begin (),prices.end ()); int cost = prices[0 ] + prices[1 ]; return cost > money?money:money-cost; } };
2023-12-30
题目传送门:1185. 一周中的第几天 - 力扣(LeetCode)
模拟题,注意判断闰年以及闰年二月份的时候即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {public : string dayOfTheWeek (int day, int month, int year) { auto judge_year = [&](int x){ if (x % 400 == 0 || (x % 4 == 0 && x % 100 != 0 )) return true ; return false ; }; vector<string> weekDay = {"Sunday" , "Monday" , "Tuesday" , "Wednesday" , "Thursday" , "Friday" , "Saturday" }; vector<int > monthDay = {31 , 28 , 31 , 30 , 31 , 30 , 31 , 31 , 30 , 31 , 30 , 31 }; int ans = day; int del_year = year-1971 ; ans += (year-1971 )*365 ; for (int i=1971 ;i<year;++i){ if (judge_year (i)) ans++; } for (int i=1 ;i<month;++i) ans += monthDay[i-1 ]; ans = (month>2 &&judge_year (year))?ans+1 :ans; int week_day = (4 +ans)%7 ; return weekDay[week_day]; } };
注意上一题Sunday存的下标为0,因为这样处理方便一些。
2023-12-31
题目传送门:1154. 一年中的第几天 - 力扣(LeetCode)
上一道题的简单版。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : int dayOfYear (string date) int year = stoi (date.substr (0 , 4 )); int month = stoi (date.substr (5 , 2 )); int day = stoi (date.substr (8 , 2 )); auto judge_year = [&](int x) { if (x%400 ==0 ||(x%4 ==0 &&x%100 !=0 )) return true ; return false ; }; vector<int > months = {31 , 28 , 31 , 30 , 31 , 30 , 31 , 31 , 30 , 31 , 30 , 31 }; int ans = day; for (int i=1 ;i<month;++i) { ans += months[i-1 ]; } return (month>2 &&judge_year (year))?ans+1 :ans; } };