我们之前所学习的知识都是监督学习，监督学习很多是基于人的经验来对分类回归问题进行判断，现在我们来研究一些关于非监督学习的内容。

首先便是一个问题，为什么我们需要研究非监督学习。

非监督学习的意义

  • 数据维度减少（Dimension reduction）
  • 预处理（Preprocessing）
  • 可视化（Visualization）
  • 更好的利用看上去不重要的数据(Taking advantage of unsupervised data)
  • 压缩，降噪，超分辨率(Compression,denoising,super-resolution)

一个可以可视化数据的网站：https://projector.tensorflow.org

总而言之就是更好的利用数据，并从数据中发现一些有用的东西。

Auto-Encoders

自编码器（autoencoder, AE）是一类在半监督学习和非监督学习中使用的神经网络（Artificial Neural Networks, ANNs），其功能是通过将输入信息作为学习目标，对输入信息进行表征学习（representation learning）

自编码器具有一般意义上表征学习算法的功能，被应用于**降维（dimensionality reduction）**和异常值检测（anomaly detection）

Auto Encoder 大致原理

  • 输入输出一样，重建输入数据
  • 中间那个很少神经元的层叫做neck（一般是对数据进行降维）

Auto Encoder就是一个非常普通的神经网络

如何训练

Loss Function

Lose function for real-valued inputs

l(f(x))=12∑k(x^k−xk)2l(f(x))=\frac{1}{2}\sum_k(\hat{x}_k-x_k)^2

  • x^k\hat{x}_k是重建后数据k位置的值
  • xkx_k是输入数据k位置的值
Loss function for binary inputs

l(f(x))=−∑k(xk log(x^k)+(1−xk)log(1−x^k))l(f(x))=-\sum_k(x_k\ log(\hat{x}_k)+(1-x_k)log(1-\hat{x}_k))

  • Cross-entropy error function

  • 一般用于分类问题，类似one-hot编码

其实还是和普通神经网络差不多

AE vs PCA

使用MNIST数据集作为输入，然后分别使用PCA或AE对数据进行降维，然后再重构，效果图如下图所示。

重构效果

人脸数据集第二行是AE，第三行是PCA，综上，可以看出AE的效果还是要好一些的。

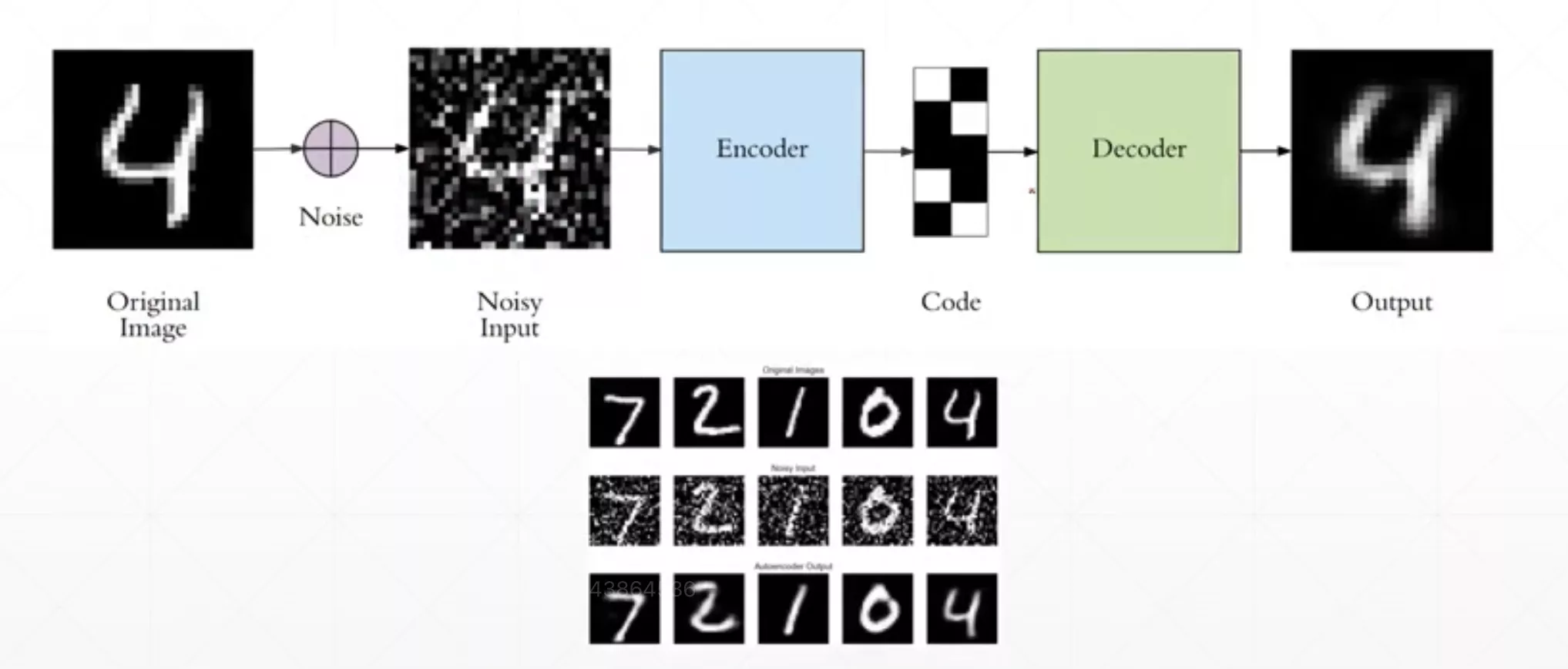
Denoising Auto-Encoders

就是对输入数据加噪声，以此让模型不要记住某些特征，而是理解某些特征，让模型发掘一些数据高层次的特征。这种类型的AE可以对图片进行降噪操作。

Denoising Auto-Encoders 原理

Dropout Auto-Encoders

正如其名，和我们前面讲的Dropout是一个意思。

Dropout Auto-Encoders

Adversarial Auto-Encoders

Adversarial Auto-Encoders

Discriminator这一部分知识涉及到GAN，会在GAN部分讲解清楚

我们目前只需要知道，随着训练次数的增加，中间的隐藏层h所得的数据会呈现出一种分布的状态。

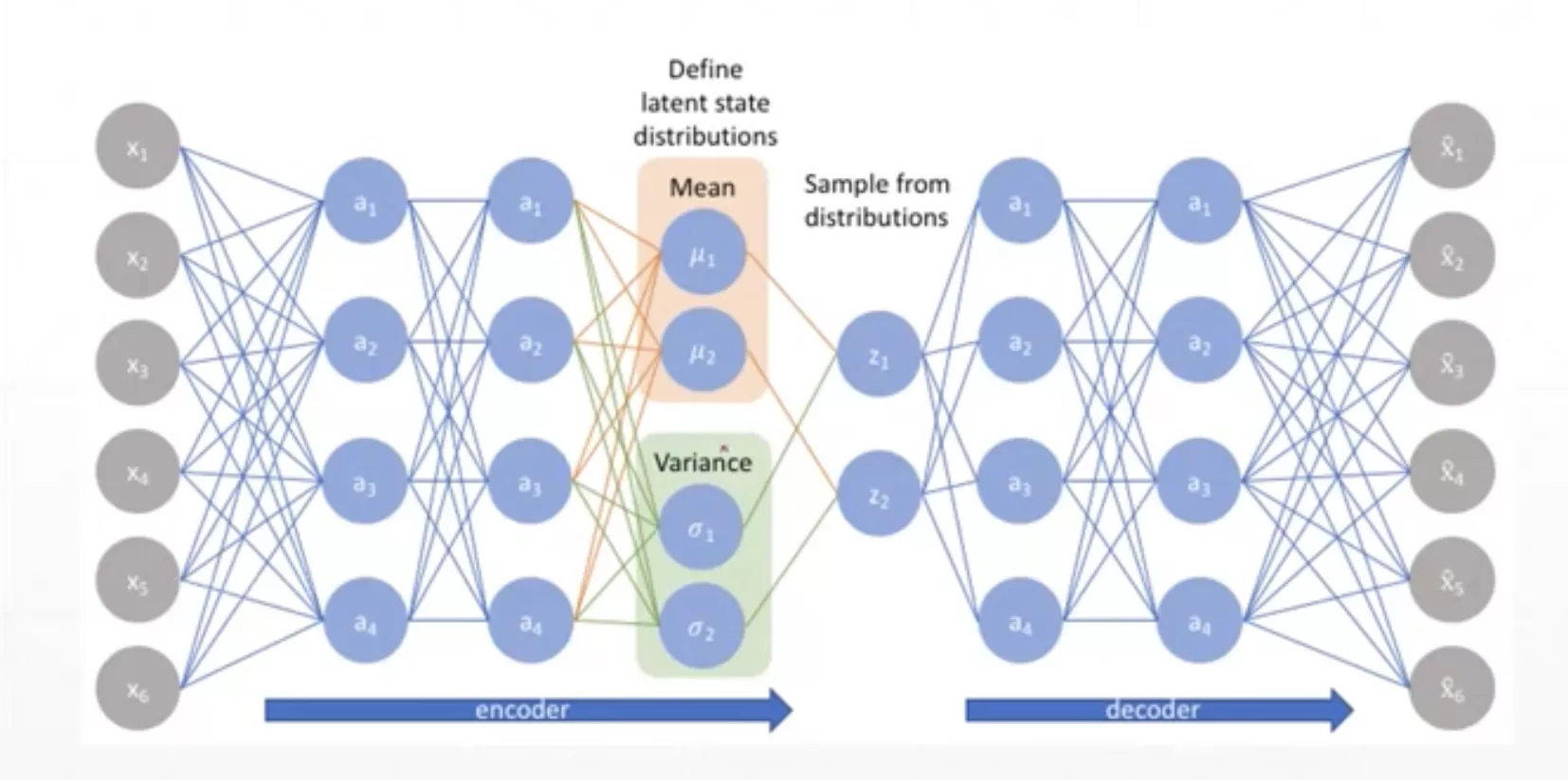
Variational Auto-Encoders（VAE）※

VAE非常的重要，具体原理可以看这个视频或这篇博客，这里就不再赘述了。（因为本人表达能力问题和比较菜，可能说不太清楚）

链接：李宏毅老师VAE原理

直观理解

VAE网络图

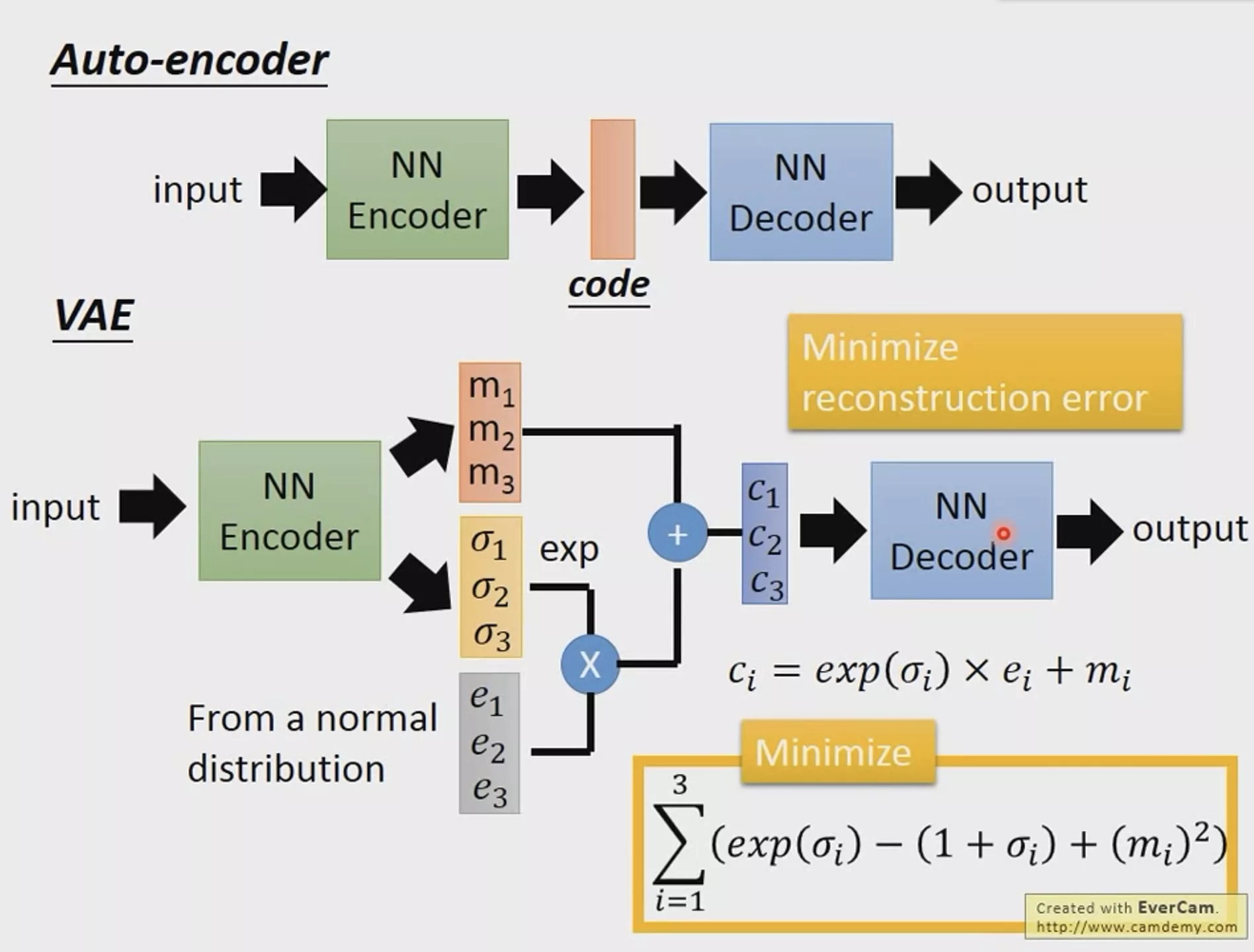
VAE原理图

注意：还是和AE不太一样，因为中间有一个采样的操作，采样的值作为提取出来的特征。因此这两层的连接也和其他层之间的连接也不一样，并不是全连接！！！

还要注意：这里我们的Loss函数不仅要最小AE中的均方差，还要最小化KL

div（上图标有Minimize的黄框），所以要将他们两个加起来作为最终的loss进行反向传播！！！（这个东西可以在上面的链接中了解到这是什么）

VAE不同于AE，学习的不是单个向量，而是分布！！！因此具有一定的推理能力，直观理解见下图的例子

Why VAE

综上，VAE虽然效果比AE好，但是根据他的原理，他本质上只是记住了现有数据的特征，并没有学习如何生成数据（只是再一个确定分布内随机），这是VAE最大的一个问题，解决这个问题需要使用我们后面马上会讲解的GAN。

GAN（右）吊打VAE（左）

Pytoch实战

Auto-Encoder实验

目标

本次实验的目标是构建一个Auto-Encoder重构MNIST数据集。

代码实现

其实代码都和最简单的全连接神经网络非常的相似，这里不再赘述，直接贴代码。

首先是网络结构的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class AE(nn.Module):

    def __init__(self) -> None:
        super(AE,self).__init__()

        # Encoder
        #  [b,784] => [b,20]
        self.encoder = nn.Sequential(
            nn.Linear(784,256),
            nn.ReLU(),
            nn.Linear(256,64),
            nn.ReLU(),
            nn.Linear(64, 20),
            nn.ReLU()
        )
        # Decoder
        # [b,20] => [b,784]
        self.decoder = nn.Sequential(
            nn.Linear(20,64),
            nn.ReLU(),
            nn.Linear(64,256),
            nn.ReLU(),
            nn.Linear(256,784),
            nn.Sigmoid()
        )
    
    def forward(self, x):

        batchsz = x.size(0)
        # flatten
        x = x.view(batchsz,784)
        # encoder
        x = self.encoder(x)
        # decoder
        x = self.decoder(x)
        # reshape
        x = x.view(batchsz,1,28,28)

        return x


注意这里我们网络结构是拆成了encoder和decoder的，这样使得网络结构更加的清晰！

训练测试部分主代码（没有区别， 只是多做了一个可视化 ）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
def main():
    mnist_train = datasets.MNIST('mnist', True, transform=transforms.Compose([
        transforms.ToTensor()
    ]), download=True)
    mnist_train = DataLoader(mnist_train,batch_size=32,shuffle=True)
    mnist_test = datasets.MNIST('mnist', False, transform=transforms.Compose([
        transforms.ToTensor()
    ]), download=True)
    mnist_test = DataLoader(mnist_test,batch_size=32,shuffle=True)

    x,_ = iter(mnist_train).next()
    print('x:', x.shape)
    
    device = torch.device('cuda')
    model = AE().to(device)
    print(model)
    criteon = nn.MSELoss()
    optimizer = optim.Adam(model.parameters(),lr=1e-3)

    viz =visdom.Visdom()

    for epoch in range(1000):

        for batchidx, (x,_) in enumerate(mnist_train):
            x = x.to(device)

            x_hat = model(x)
            loss = criteon(x_hat,x)

            # backprop
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

        print(epoch , "loss:", loss.item())

        x,_ = iter(mnist_test).next()
        x = x.to(device)
        with torch.no_grad():
            x_hat = model(x)
        viz.images(x,nrow=8,win='x',opts=dict(title='x'))
        viz.images(x_hat,nrow=8,win='x_hat',opts=dict(title='x_hat'))

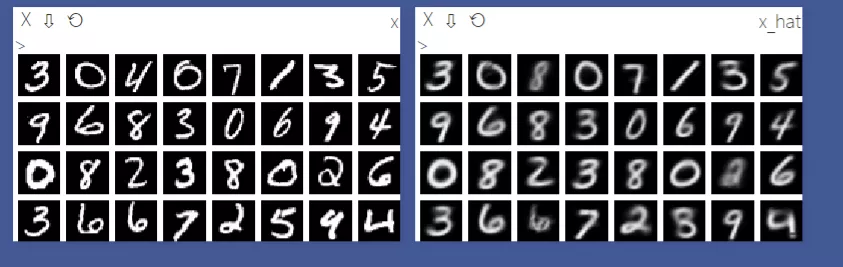
结果

重建结果如下图所示，尽管这个数据集非常的简单，但是我们还是可以看出，还是有一些数据重建的并不是非常的理想。

重建结果

VAE实验

目标

本次实验的目标是构建一个VAE重构MNIST数据集。

因为VAE中间有一个操作是采样，而采样这个操作是不可导的，因此在实际代码实现中这里有一个小trick。

代码实现

网络结构代码和AE代码是一样的（还是有一点不一样 decoder起始神经元数量变为10，注意改一下！ ），不一样的部分体现在forward部分（在encoder和decoder中间增加了采样），这里就使用到了我们的trick，利用pytorch自带的分布生成器，可以生成可导的采样操作。注意forward最后返回了kld哦！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()


        # [b, 784] => [b, 20]
        # u: [b, 10]
        # sigma: [b, 10]
        self.encoder = nn.Sequential(
            nn.Linear(784, 256),
            nn.ReLU(),
            nn.Linear(256, 64),
            nn.ReLU(),
            nn.Linear(64, 20),
            nn.ReLU()
        )
        # [b, 20] => [b, 784]
        self.decoder = nn.Sequential(
            nn.Linear(10, 64),
            nn.ReLU(),
            nn.Linear(64, 256),
            nn.ReLU(),
            nn.Linear(256, 784),
            nn.Sigmoid()
        )

        self.criteon = nn.MSELoss()

    def forward(self, x):
        """

        :param x: [b, 1, 28, 28]
        :return:
        """
        batchsz = x.size(0)
        # flatten
        x = x.view(batchsz, 784)
        # encoder
        # [b, 20], including mean and sigma
        h_ = self.encoder(x)
        # [b, 20] => [b, 10] and [b, 10]
        mu, sigma = h_.chunk(2, dim=1)
        # reparametrize trick, epison~N(0, 1)
        h = mu + sigma * torch.randn_like(sigma)

        # decoder
        x_hat = self.decoder(h)
        # reshape
        x_hat = x_hat.view(batchsz, 1, 28, 28)

        kld = 0.5 * torch.sum(
            torch.pow(mu, 2) +
            torch.pow(sigma, 2) -
            torch.log(1e-8 + torch.pow(sigma, 2)) - 1
        ) / (batchsz*28*28)

        return x_hat, kld

然后就是训练部分的代码了，这里也就只有loss函数改了一下。

1
2
3
4
5
x_hat, kld = model(x)
loss = criteon(x_hat, x)
if kld is not None:
    elbo = - loss - 1.0 * kld
    loss = - elbo

完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
def main():
    mnist_train = datasets.MNIST('mnist', True, transform=transforms.Compose([
        transforms.ToTensor()
    ]), download=True)
    mnist_train = DataLoader(mnist_train, batch_size=32, shuffle=True)


    mnist_test = datasets.MNIST('mnist', False, transform=transforms.Compose([
        transforms.ToTensor()
    ]), download=True)
    mnist_test = DataLoader(mnist_test, batch_size=32, shuffle=True)


    x, _ = iter(mnist_train).next()
    print('x:', x.shape)

    device = torch.device('cuda')
    # model = AE().to(device)
    model = VAE().to(device)
    criteon = nn.MSELoss()
    optimizer = optim.Adam(model.parameters(), lr=1e-3)
    print(model)

    viz = visdom.Visdom()

    for epoch in range(1000):


        for batchidx, (x, _) in enumerate(mnist_train):
            # [b, 1, 28, 28]
            x = x.to(device)

            x_hat, kld = model(x)
            loss = criteon(x_hat, x)

            if kld is not None:
                elbo = - loss - 1.0 * kld
                loss = - elbo

            # backprop
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()


        print(epoch, 'loss:', loss.item(), 'kld:', kld.item())

        x, _ = iter(mnist_test).next()
        x = x.to(device)
        with torch.no_grad():
            x_hat, kld = model(x)
        viz.images(x, nrow=8, win='x', opts=dict(title='x'))
        viz.images(x_hat, nrow=8, win='x_hat', opts=dict(title='x_hat'))

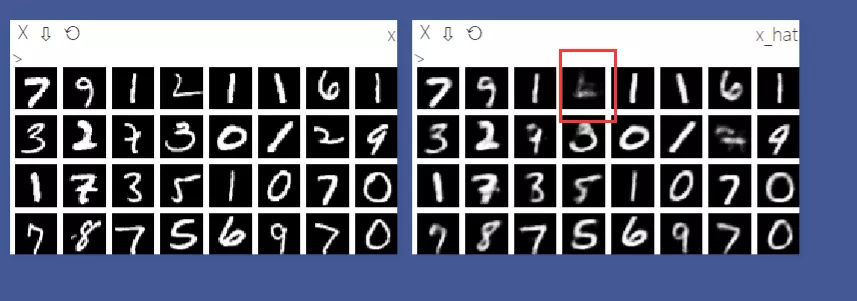
结果

重建结果如下图所示，VAE重建的所有数字基本上是可以看清楚的，但是因为此数据集比较简单的缘故，VAE相比于AE的优势并没有很好的体现出来。

VAE结果

本站由 @anonymity 使用 Stellar 主题创建。
本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。