PyTorch：PyTorch过拟合

过拟合与欠拟合

一张图说清过拟合与欠拟合

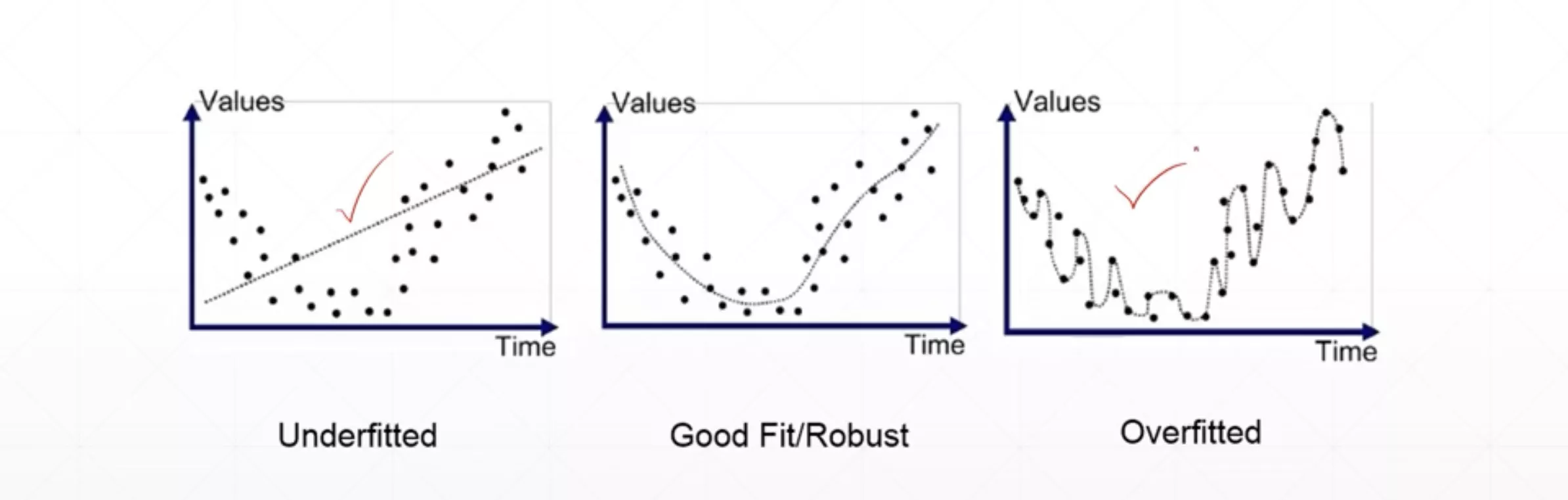
欠拟合

训练时的准确率低（train acc. is bad）
测试时的准确率也很低（test acc. is bad as well）

过拟合

相比于欠拟合的状态，训练时的损失函数和准确率要好得多（train loss and acc. is much better）
测试时的准确率要低一些(test acc. is worse)
泛化能力较差（generalization performance is worse）

Train-Val-Test划分

使用如Train-Val-Test划分来检测是否存在过拟合或者欠拟合的情况。

Train：用来训练网络

Val：用来挑选模型参数，用于监视训练（几轮训练后跑一轮Val），发现过拟合时可以提前停止训练模型 Test：验证模型最终的性能（给客户看），一般实际情况下这一部分的数据客户不会提供

PyTorch划分Train-Val数据集代码如下：

print('train:',len(train_db),'test:',len(test_db))
train_db,val_db=torch.utils.data.random_split(train_db,[50000,10000])
print('db1:',len(train_db),'db2:',len(val_db))
train_loader=torch.utils.data.DataLoader(
    train_db,
    batch_size=batch_size,shuffle=True
)
val_loader=torch.utils.data.DataLoader(
    val_db,
    batch_size=batch_size,shuffle=True
)

k折交叉验证（k-fold cross validation）

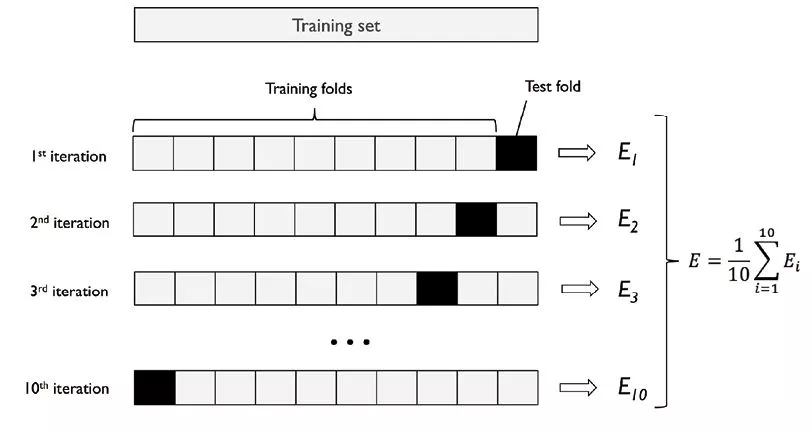
K-fold交叉验证是一种数据拆分技术，被定义为一种用于在未见过的数据上估计模型性能的方法。你可以使用k>1折来实现用于不同目的的样本划分，也是一种用于超参数优化的技术，以便可以训练具有最优超参数值的模型。这是一种无需增添或者修改样本的重采样技术。这种方法的优点是，每个样本案例仅用于训练和验证（作为测试折的一部分）一次。与传统方法相比，这种方法可以很好降低模型性能的方差。

K-fold交叉验证的过程分为下面几步：

把数据集分为训练数据集和测试数据集。
然后将训练数据集拆分为K份；在K-folds样本中，（K-1）份用于训练，1份用于验证，把每次模型的性能记录下来。
重复第2步，直到每个k-fold 都用到了验证（这就是为什么它被称为k-fold交叉验证）。
通过获取步骤2中为所有K个模型计算的模型分数来计算模型性能的均值和标准差。
对不同的超参数值重复步骤2到步骤5。
最后选择产生最优分数均值和标准值的模型超参数。
在测试数据集上计算评估模型性能。

计算使用K折训练的模型性能的平均分数

汇总

仍然是针对MINST数据集，基于前面优化的基础上但是划分成为了三个数据集的代码：

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms


batch_size=200
learning_rate=0.01
epochs=10

train_db = datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ]))
train_loader = torch.utils.data.DataLoader(
    train_db,
    batch_size=batch_size, shuffle=True)

test_db = datasets.MNIST('../data', train=False, transform=transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307,), (0.3081,))
]))
test_loader = torch.utils.data.DataLoader(test_db,
    batch_size=batch_size, shuffle=True)


print('train:', len(train_db), 'test:', len(test_db))
train_db, val_db = torch.utils.data.random_split(train_db, [50000, 10000])
print('db1:', len(train_db), 'db2:', len(val_db))
train_loader = torch.utils.data.DataLoader(
    train_db,
    batch_size=batch_size, shuffle=True)
val_loader = torch.utils.data.DataLoader(
    val_db,
    batch_size=batch_size, shuffle=True)




class MLP(nn.Module):

    def __init__(self):
        super(MLP, self).__init__()

        self.model = nn.Sequential(
            nn.Linear(784, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 10),
            nn.LeakyReLU(inplace=True),
        )

    def forward(self, x):
        x = self.model(x)

        return x

device = torch.device('cuda:0')
net = MLP().to(device)
optimizer = optim.SGD(net.parameters(), lr=learning_rate)
criteon = nn.CrossEntropyLoss().to(device)
# Train部分
for epoch in range(epochs):

    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.view(-1, 28*28)
        data, target = data.to(device), target.cuda()

        logits = net(data)
        loss = criteon(logits, target)

        optimizer.zero_grad()
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))

	# Val验证部分
    test_loss = 0
    correct = 0
    for data, target in val_loader:
        data = data.view(-1, 28 * 28)
        data, target = data.to(device), target.cuda()
        logits = net(data)
        test_loss += criteon(logits, target).item()

        pred = logits.data.max(1)[1]
        correct += pred.eq(target.data).sum()

    test_loss /= len(val_loader.dataset)
    print('\nVAL set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(val_loader.dataset),
        100. * correct / len(val_loader.dataset)))


# test测试部分
test_loss = 0
correct = 0
for data, target in test_loader:
    data = data.view(-1, 28 * 28)
    data, target = data.to(device), target.cuda()
    logits = net(data)
    test_loss += criteon(logits, target).item()

    pred = logits.data.max(1)[1]
    correct += pred.eq(target.data).sum()

test_loss /= len(test_loader.dataset)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
    test_loss, correct, len(test_loader.dataset),
    100. * correct / len(test_loader.dataset)))

减少过拟合的方法

更多的数据（More Data）
减少模型的复杂程度（Constraint model complexity）
- 更浅的网络
- 正则化
Dropout
数据增强（Data aargumentation）
Early stopping（前面进行讲解过）

正则化（Regularization）

你可能熟悉奥卡姆剃刀原则：给出两个解释，最可能正确的解释是更简单的一个 – 假设较少的解释。这个原则也适用于神经网络的模型： 简单的模型比复杂的泛化能力好。

正则化，即在成本函数中加入一个正则化项(惩罚项)，惩罚模型的复杂度，防止网络过拟合。

以Logistic Regression的交叉熵损失函数为例。

J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y_i ln\hat{y}_i+(1-y_i)ln(1-\hat{y}_i)]

我们加入对参数的惩罚项

J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y_i ln\hat{y}_i+(1-y_i)ln(1-\hat{y}_i)]+\lambda\sum_{i=1}^n|\theta_i|

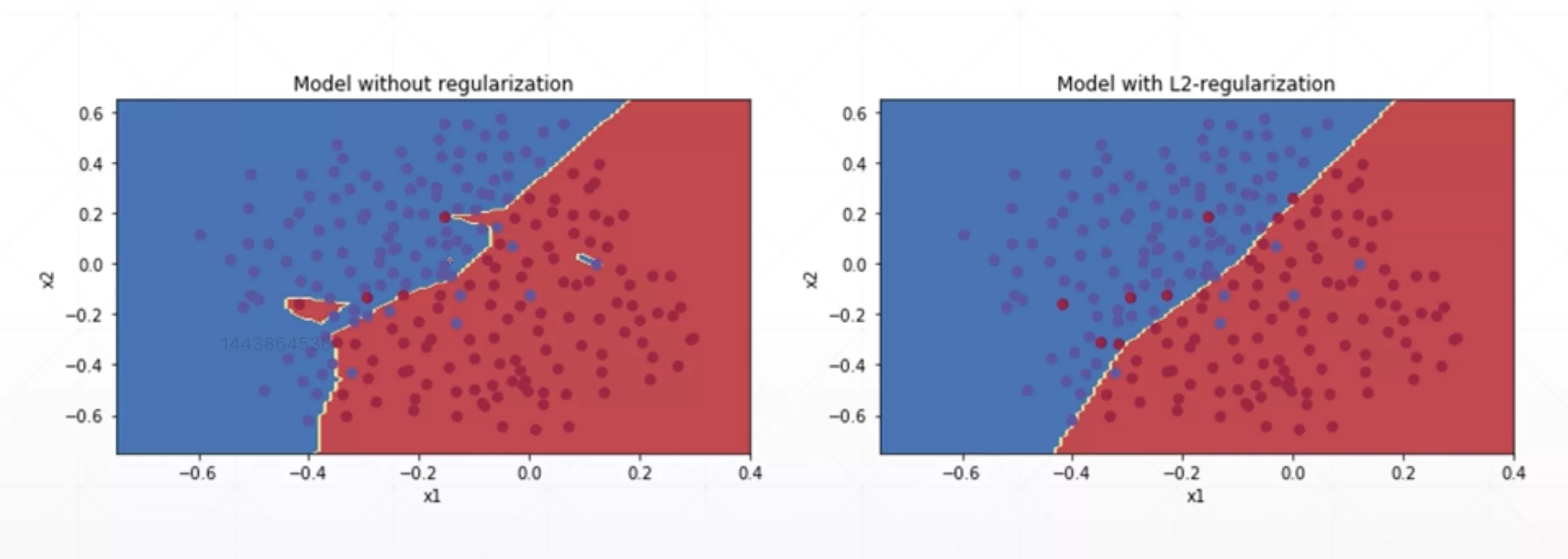
当然也可以加L2范数的惩罚项(在PyTorch中最常用)

J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y_i ln\hat{y}_i+(1-y_i)ln(1-\hat{y}_i)]+\frac{1}{2}\lambda\sum_{i=1}^n||\theta_i||^2

这样通过调整合适的 $\lambda$ 参数就可以有效的抑制模型高阶参数。

正则化在PyTorch中又叫做`Weight

Decay`

在PyTorch中做L2-regularization

device=torch.device('cuda:0')
net=MLP().to(device)
optimizer=optim.SGD(net.parameters(),lr=learning_rate,weight_decay=0.01)#这里加一个weight_decay参数就好了
criteon=nn.CrossEntropyLoss().to(device)

在PyTorch中做L1-regularization

因为PyTorch不提供相应的API，所以L1-regularization需要自己实现.

regularization_loss=0
for param in model.parameters():
    regularization_loss+=torch.sum(torch.abs(param))

classify_loss=criteon(logits,target)
loss=classify_loss+0.01*regularization_loss

optimizer.zero_grad()
loss.backward()
optimizer.step()

一般是出现了overfitting的情况后才会设置weight_decay

不正则化与正则化的对比图

动量与学习率衰减

动量（momentum）
学习率衰减（learningrate decay）

动量（momentum）

原来的更新函数

w^{k+1}=w^k-\alpha\nabla f(w^k)

加了动量以后的更新函数

w^{k+1}=w^k-\alpha z^{k+1}

z^{k+1}=\beta z^k+\nabla f(w^k)

$z^k$ 在这里代表上一次梯度的方向，所以每次的更新不仅取决于这一次梯度的方向还要取决于上一次梯度的方向。可以发现动量其实就是指数加权平均。

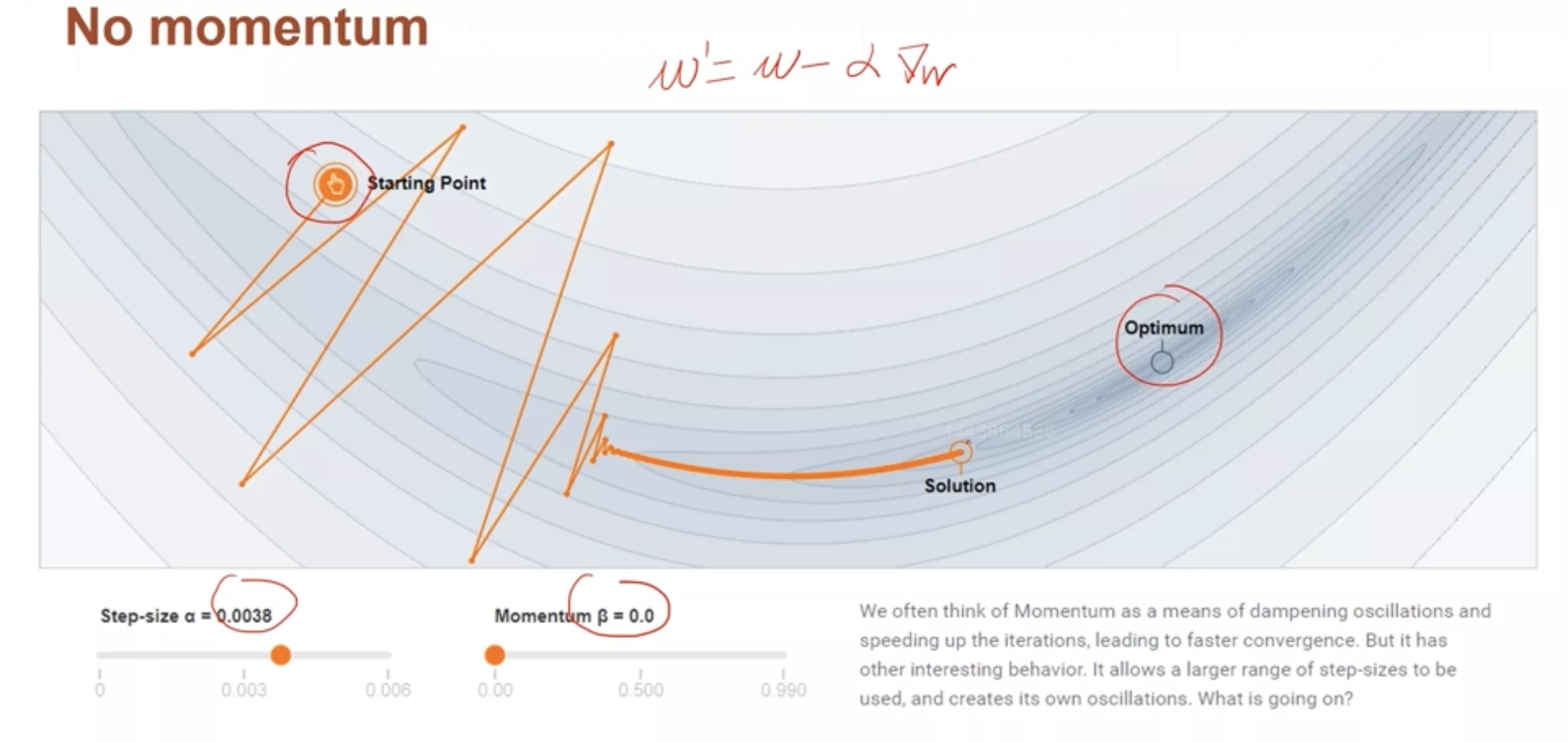
未添加动量

有动量

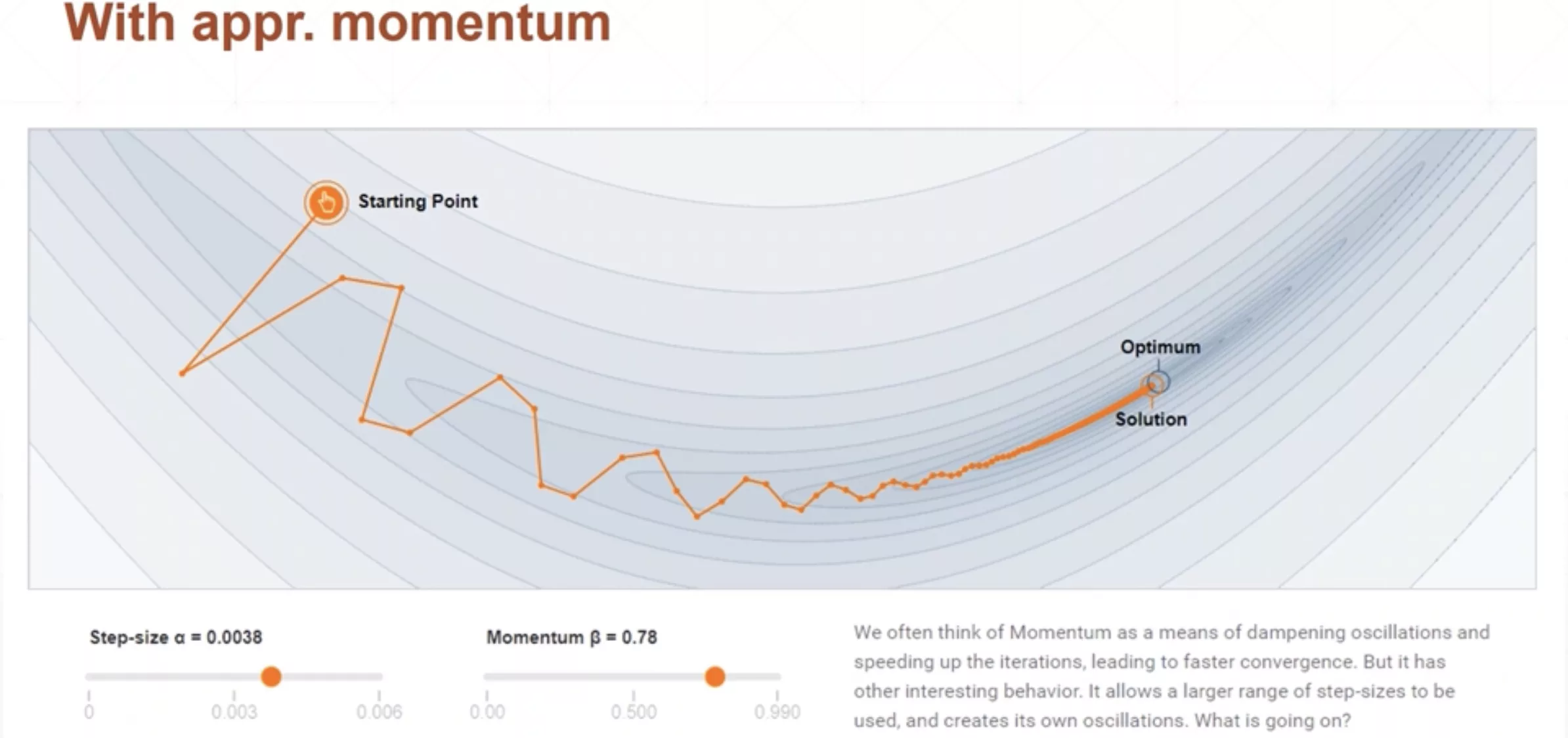
可以发现相比未添加动量，有动量的训练更新的时候方向变化没有那么尖锐和剧烈了，未添加动量的训练最终无法收敛到最优解，但是添加了动量的训练，最终可以凭借惯性得到全局最优解。

PyTorch对momentum的支持

optimizer=torch.optim.SGD(model.parameters(),args.lr,
                                    momentum=args.momentum,# 这里添加一个动量参数就可以了
                                    weight_decay=args.weight_decay)
scheduler=ReduceLROnPlateau(optimizer,'min')

for epoch in xrange(args.start_epoch,args.epochs):
    train(train_loader,model,criterion,optimizer,epoch)
    reult_avg,loss_val=validate(val_loader,model,criterion,epoch)
    scheduler.step(loss_val)

学习率衰减（learningrate decay）

学习率衰减一般有两种衰减策略

一种是当损失函数碰到平原的时候进行学习率衰减，使用PyTorch中的函数是ReduceLROnPlateau

optimizer=torch.optim.SGD(model.parameters(),args.lr,
                                    momentum=args.momentum,# 这里添加一个动量参数就可以了
                                    weight_decay=args.weight_decay)
scheduler=ReduceLROnPlateau(optimizer,'min')

for epoch in xrange(args.start_epoch,args.epochs):
    train(train_loader,model,criterion,optimizer,epoch)
    reult_avg,loss_val=validate(val_loader,model,criterion,epoch)
    scheduler.step(loss_val)

还有一种比较简单粗暴，就是每过多少步然后把learning_rate进行衰减。PyTorch中使用的函数是StepLR

# Assuming optimizer uses lr = 0.05 for all groups
# lr = 0.05   if epoch < 30
# lr = 0.005  if 30 <= epoch < 60
# lr = 0.0005 if 60 <= epoch < 90
schedular =StepLR(optimizer,steo_size=30,gamma=0.1)
for epoch in range(100):
    scheduler.step()
    train(...)
    validate(...)

StepLR中的参数表示的就是每步进30步，lr减少为原来的0.1，详情可以见上面的代码注释。

Early Stop&Dropout

Early Stop

因为有时训练轮数过多会出现过拟合的情况从而让模型性能变坏，所以在必要的时候我们要先停止训练模型（val取最大值时），保存参数，避免继续训练出现过拟合的情况。这就是我们所说的Early Stop

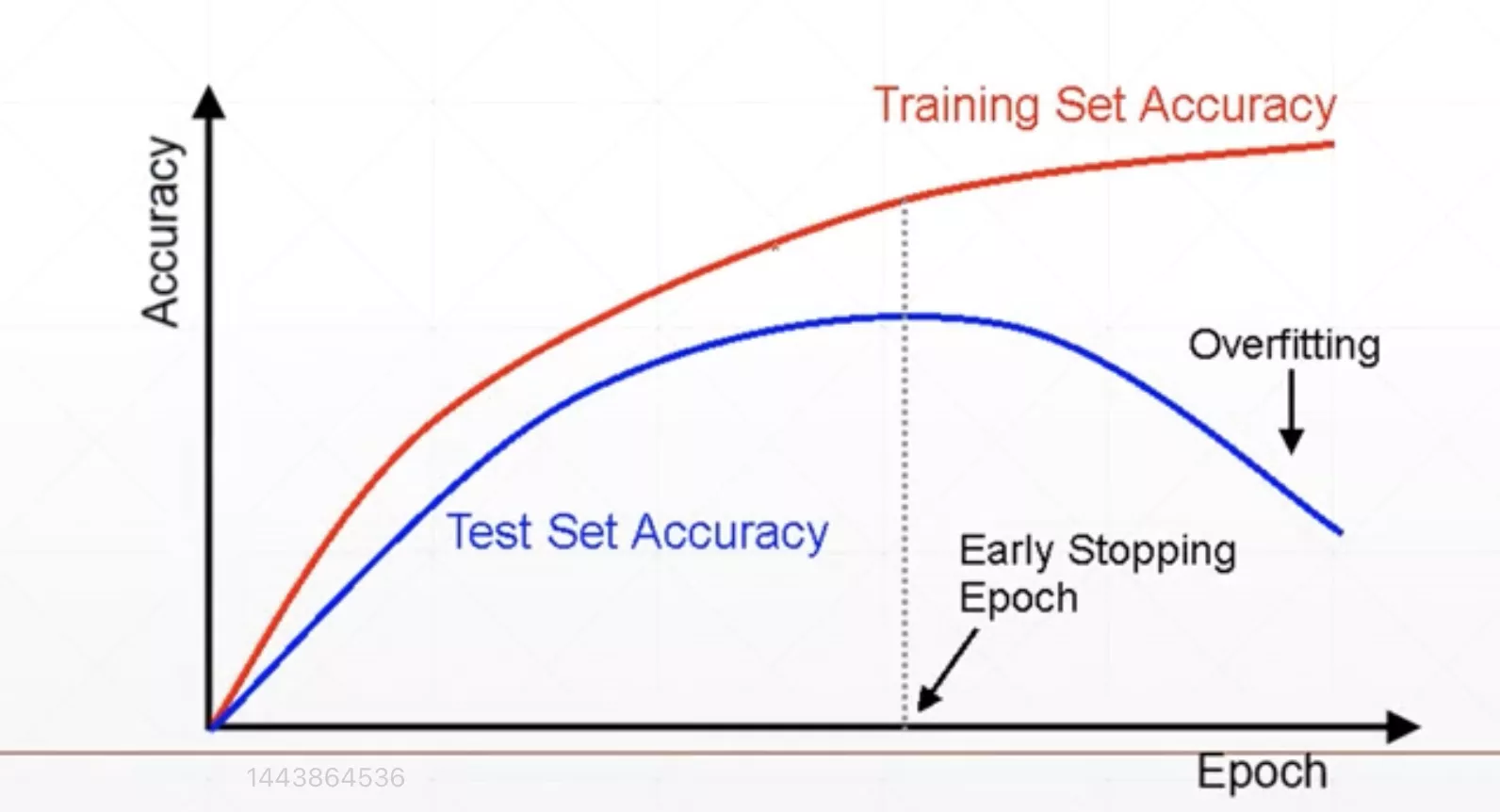
过拟合情况

步骤

Val数据集用来选择参数（超参数）
观察验证集的表现
在Val验证集Acc最高（或Loss最低）处停止训练（根据经验，连续下滑一段时间后我们就认为前面的最高点就是最好的）

Dropout

思想

学的更少来学的更好
每个连接都有p的概率被断开

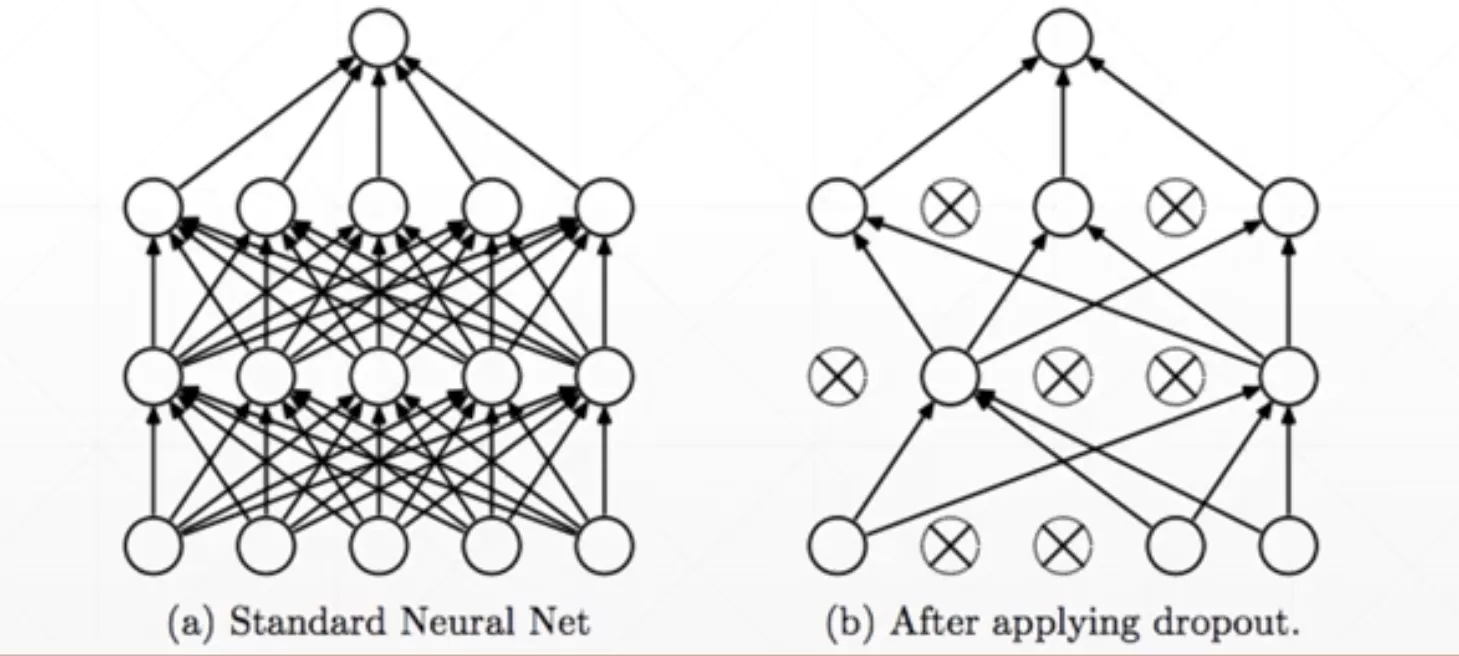
Dropout原理图

代码实现

PyTorch中添加Dropout还是比较方便的

net_dropped=torch.nn.Sequential(
    torch.nn.Linear(784,200),
    torch.nn.Dropout(0.5),
    torch.nn.ReLU(),
    torch.nn.Linear(200,200),
    torch.nn.Dropout(0.5),
    torch.nn.ReLU(),
    torch.nn.Linear(200,10),
)

层之间是直连的，这里的意思是在层之间有50%的概率出现连接断掉。和上面画的示意图有一点不一样。

注意：dropout只在训练的时候才有，测试的时候是不会dropout的。

数据增强

见PyTorch CNN,因为讲解了卷积神经网络在图像识别方面的应用后，可能会对这一方面印象更加深刻一些。

SGD

SGD全称Stochastic Gradient Descent，中文全称叫随机梯度下降。为了解决数据集过大无法将所有样本放入进行梯度下降，我们将数据集化成若干个Batch，一个Batch中包含若干个样本，每次使用一个Batch进行一次梯度下降（注意是一个Batch而不是每次取一个样本就下降一次）

其实以上这个应该叫做小批量梯度下降，而并非SGD

，SGD是Batchsize=1的小批量梯度下降。这里推荐一篇讲解不同梯度下降的博客：机器学习：面对海量数据如何进行机器学习