卷积神经网络结构介绍

如果用全连接神经网络处理大尺寸图像具有三个明显的缺点：

（1）首先将图像展开为向量会丢失空间信息；

（2）其次参数过多效率低下，训练困难；

（3）同时大量的参数也很快会导致网络过拟合。

而使用卷积神经网络可以很好地解决上面的三个问题。

卷积神经网络的提出参考了人眼的局部相关性，人眼用于识别物体也是先看一个局部，根据一些特称才能辨别这个物体是什么，特征的识别和像素点的排列位置和情况有关。

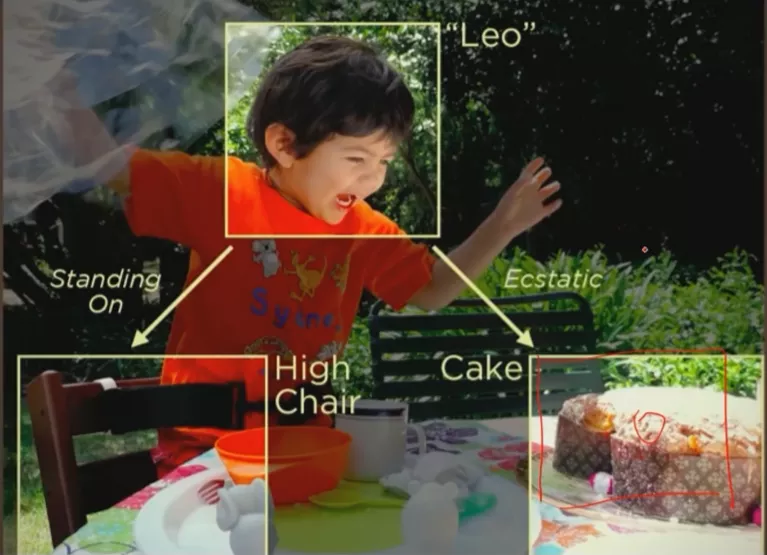
人眼识别物体局部相关性

根据局部相关性提出的卷积神经网络结构

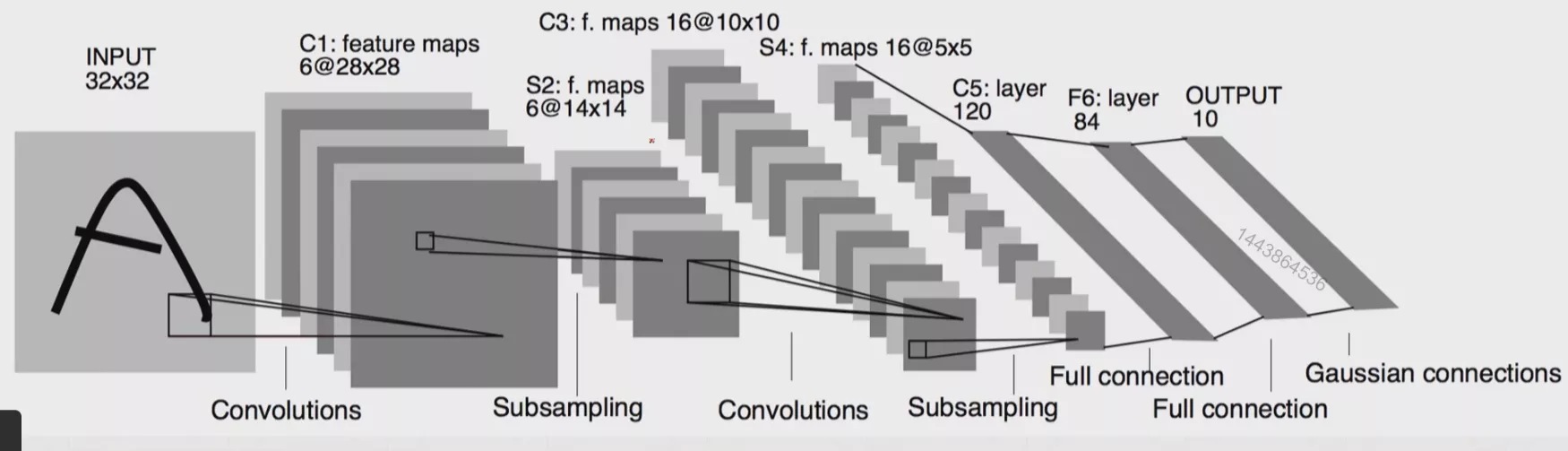
卷积神经网络结构

卷积运算

首先我们使用几张图来直观感受一下卷积是如何运算的

卷积运算

卷积运算Ⅱ

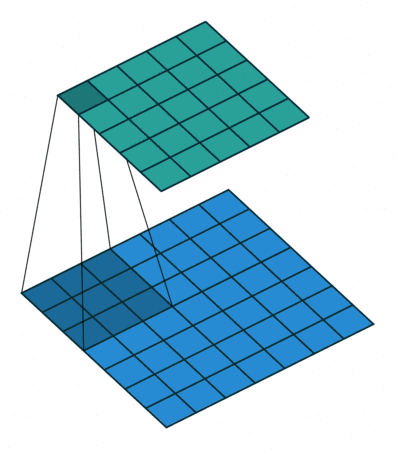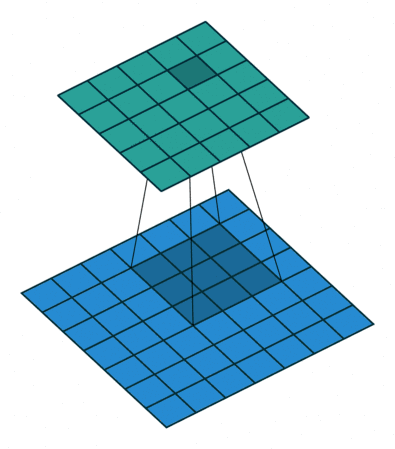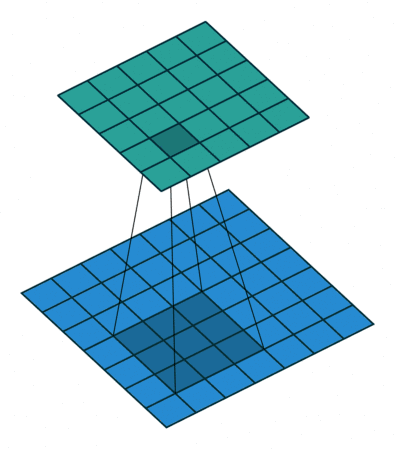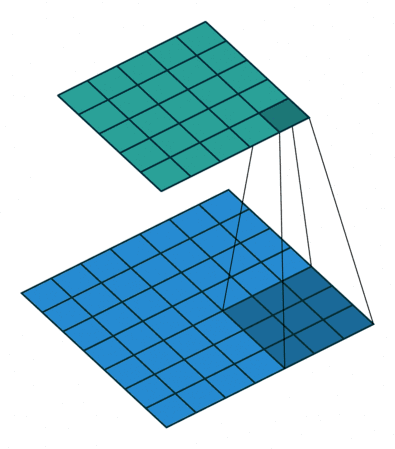
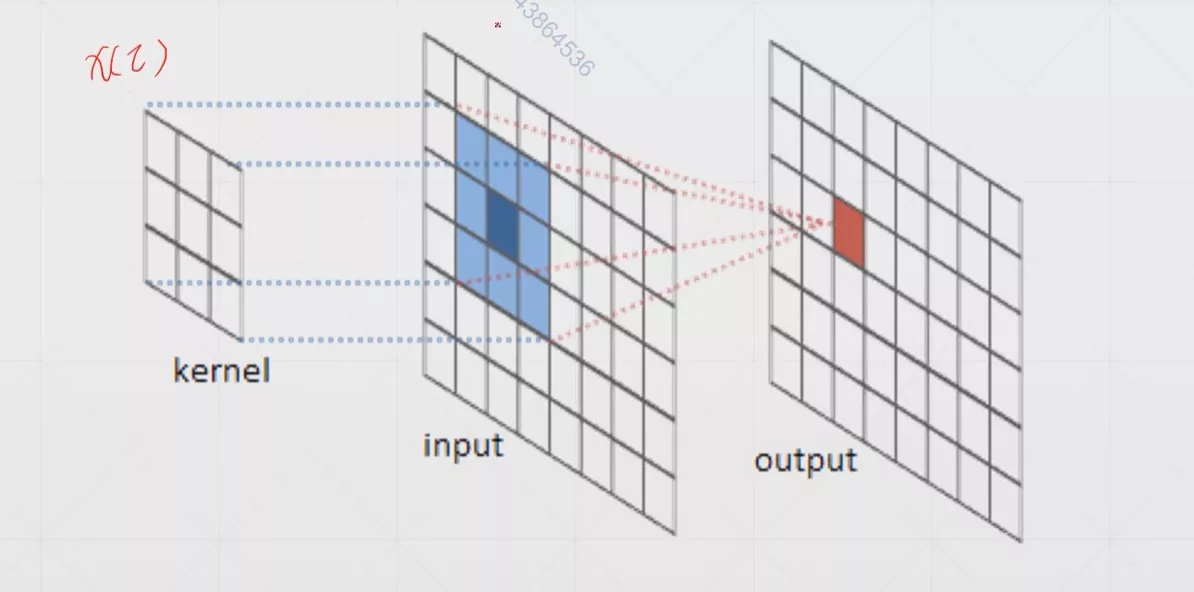
卷积运算示意图

最左边的那个叫做卷积核

更多更详细关于卷积神经网络的基础知识可以访问如下这篇博客：深度学习：卷积神经网络（CNN

常用卷积核

锐化

模糊

边缘检测

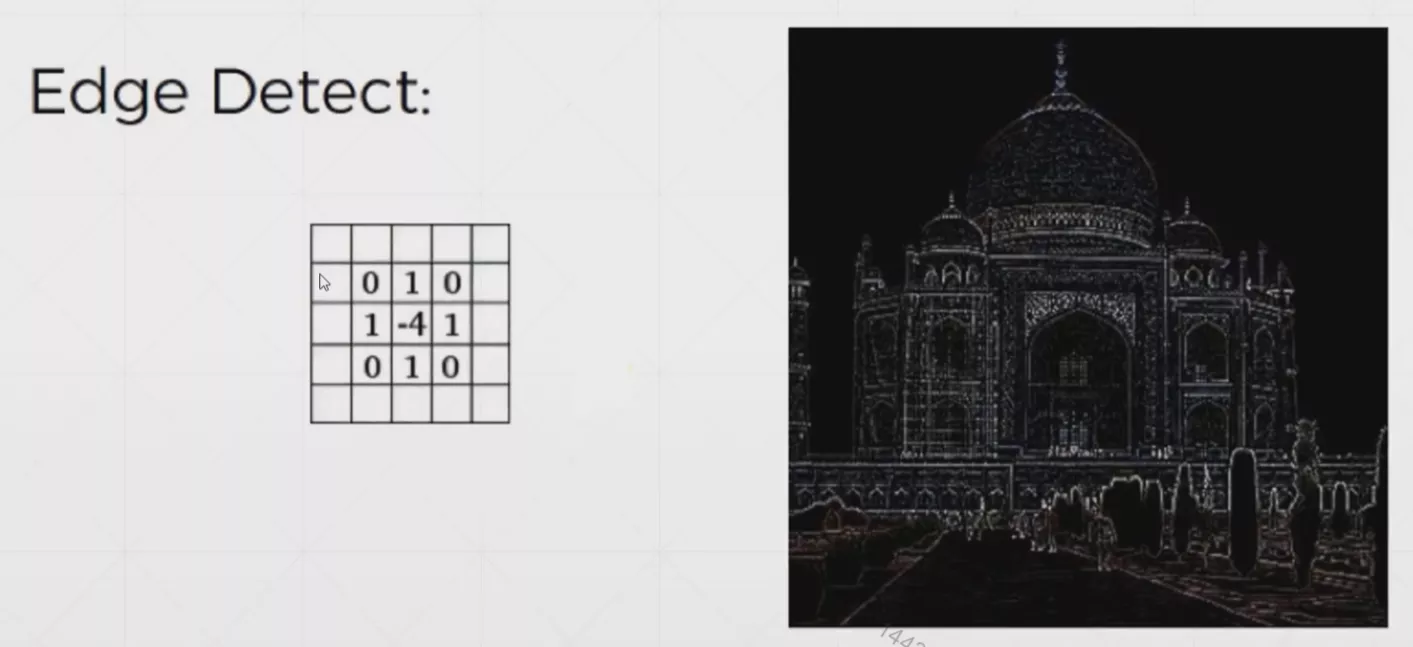
概念解析

输入通道（Input_channels）:输入有多少个通道（多少层输入），比如如果我们使用的是黑白照片，那么就只有一个通道；如果我们使用的是rgb彩色照片那么就有三个通道。

**核通道（Kernel_channels）:**卷积核有多少个通道数量。

核大小（Kernel_size）:卷积核的大小，一般是3×3

步长（Stride）:每次卷积核移动的步长，一般默认是1

填充（Padding）:为了保证卷积运算每次卷积完成以后输入输出图片大小相同，我们可能需要在图片周围填充一圈0。

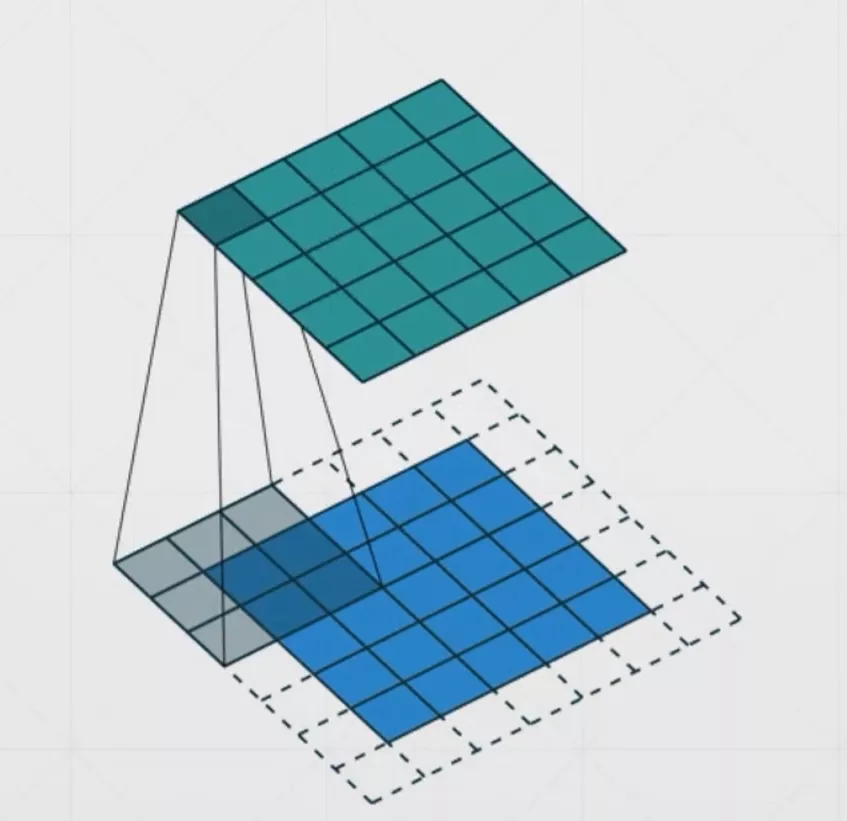
打Padding的效果

对于每一个卷积核，其所包含的通道数必须和输入的卷积层的通道数一样！所以上面核通道有两种含义，一种是指每一个卷积核中所含的通道数，还有一种含义是指有多少个卷积核。

但是一般情况下都是指后者。

因此对于b个28×28，3通道的输入x: [b,3,28,28]如果我们采用16个3*3的卷积核，则对于一个卷积核他的size是one-k: [3,3,3],对于16个k的总size是multi-k: [16,3,3,3],因为有16个卷积核所以偏置也有16个bias: [16](这里运用了广播)。最终的输出是out: [b,16,28,28]（考虑了padding）

PyTorch实现

了解了基本的卷积神经网络后，下面我们尝试使用PyTorch简单的实现一个简单的二维卷积神经网络，所使用的函数是nn.Conv2d其中第一个参数表示的是输入的通道数，后面的参数表示的是输出的通道数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
In [3]: import torch.nn as nn
In [4]: layer=nn.Conv2d(1,3,kernel_size=3,stride=1,padding=0)
In [5]: x=torch.rand(123,1,28,28)
In [6]: out=layer.forward(x)
In [7]: out.shape
Out[7]: torch.Size([123, 3, 26, 26])
In [8]: layer=nn.Conv2d(1,12,kernel_size=3,stride=1,padding=1)
In [9]: out=layer.forward(x)
In [10]: out.shape
Out[10]: torch.Size([123, 12, 28, 28])
In [11]: layer=nn.Conv2d(1,12,kernel_size=3,stride=2,padding=1)
In [12]: out=layer.forward(x)
In [13]: out.shape
Out[13]: torch.Size([123, 12, 14, 14])
In [14]: out=layer(x) # 强烈推荐这一种不使用forward的方法
In [15]: out.shape
Out[15]: torch.Size([123, 12, 14, 14])

我们也可以使用下面的代码来看看最后一次这个layer中存放了什么样的weight和bias(接上面的代码)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
In [16]: layer.weight
Out[16]: 
Parameter containing:
tensor([[[[-0.2432, -0.2371,  0.2480],
          [-0.2706, -0.2552, -0.0627],
          [ 0.1960, -0.3049, -0.0273]]],
        [[[-0.3008,  0.1268,  0.0518],
          [ 0.0673,  0.2716, -0.1481],
          [ 0.1075, -0.2905,  0.1106]]],
        [[[ 0.1498, -0.0681, -0.1162],
          [ 0.3015,  0.1400,  0.0372],
          [-0.1401,  0.1158, -0.0872]]],
        [[[ 0.1543, -0.0323, -0.2023],
          [ 0.2972, -0.0344,  0.3114],
          [ 0.2141, -0.0388, -0.0352]]],
        [[[ 0.1029,  0.0184, -0.2372],
          [ 0.2758, -0.1239,  0.2429],
          [-0.0263, -0.2977, -0.2075]]],
        [[[ 0.2166, -0.1031, -0.2122],
          [ 0.2123, -0.1492, -0.0831],
          [-0.0155, -0.0572, -0.2485]]],
        [[[-0.0441, -0.3298,  0.2896],
          [ 0.1438,  0.1364, -0.2721],
          [ 0.0076,  0.0919, -0.1219]]],
        [[[ 0.3241,  0.1343,  0.0140],
          [ 0.2732, -0.1690, -0.3122],
          [ 0.2933,  0.0007,  0.1548]]],
        [[[ 0.2695,  0.3256,  0.0424],
          [-0.2905, -0.1272, -0.1482],
          [-0.1993,  0.1244,  0.1924]]],
        [[[ 0.1136, -0.0931, -0.2240],
          [-0.0278, -0.1714, -0.0614],
          [-0.0067, -0.1385, -0.2265]]],
        [[[ 0.3065,  0.1684, -0.0113],
          [-0.0534,  0.0034,  0.0194],
          [-0.1013,  0.0573, -0.2356]]],
        [[[-0.1154, -0.0406,  0.0382],
          [-0.3318, -0.2613,  0.0636],
          [-0.2066,  0.3052, -0.2338]]]], requires_grad=True)
In [17]: layer.weight.shape
Out[17]: torch.Size([12, 1, 3, 3])
In [18]: layer.bias.shape
Out[18]: torch.Size([12])

以上是类API的写法，PyTorch也提供函数API，具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
In [3]: import torch.nn.functional as F
In [4]: w=torch.rand(16,3,5,5,requires_grad=True)
In [5]: b=torch.rand(16,requires_grad=True)
In [6]: x=torch.rand(321,3,28,28)
In [7]: out=F.conv2d(x,w,b,stride=1,padding=1)
In [8]: out.shape
Out[8]: torch.Size([321, 16, 26, 26])
In [9]: out=F.conv2d(x,w,b,stride=2,padding=2)
In [10]: out.shape
Out[10]: torch.Size([321, 16, 14, 14])

池化层与采样

下采样（Downsample）

下采样示意图

就是将下面的这个大矩阵变成上面的那个小矩阵，其实下采样和是缩小图片有点像

Max Pooling

Max Pooling和下采样类似，但是是每次观察一个区域后取该区域值最大的值为该区域的采样值

Max Pooling原理图（stride=2）

类似的还有Avg

Pooling

PyTorch 实现

PyTorch同样提供两种类型的API，这里所使用的函数是nn.MaxPool2d和nn.AvgPool2d和avg_pool2d和max_pool2d

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
In [3]: import torch.nn as nn
In [4]: x=torch.rand(123,16,14,14)
In [5]: layer=nn.MaxPool2d(2,stride=2)
In [6]: out=layer(x)
In [7]: out.shape
Out[7]: torch.Size([123, 16, 7, 7])
In [8]: layer=nn.AvgPool2d(2,stride=2)
In [9]: out=layer(x)
In [10]: out.shape
Out[10]: torch.Size([123, 16, 7, 7])
In [11]: import torch.nn.functional as F
In [12]: out=F.max_pool2d(x,2,stride=2)
In [13]: out.shape
Out[13]: torch.Size([123, 16, 7, 7])
In [14]: out=F.avg_pool2d(x,2,stride=2)
In [15]: out.shape
Out[15]: torch.Size([123, 16, 7, 7])

上采样（Upsample）

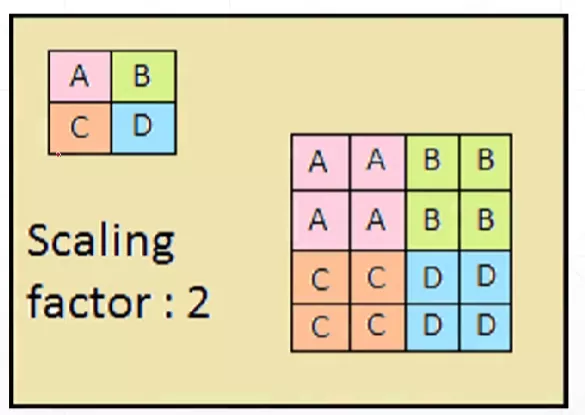
上采样示意图

就是将上面的这个小矩阵变成下面的那个大矩阵，相当于图片的放大，和下采样正好相反

PyTorch 实现

上采样所使用的函数是interpolate函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
In [3]: import torch.nn.functional as F
In [4]: x=torch.rand(1,1,3,3)
In [5]: x
Out[5]: 
tensor([[[[0.0565, 0.2834, 0.3705],
          [0.4337, 0.8775, 0.8109],
          [0.8081, 0.8048, 0.3552]]]])
In [6]: out=F.interpolate(x,scale_factor=2,mode='nearest')
In [7]: out
Out[7]: 
tensor([[[[0.0565, 0.0565, 0.2834, 0.2834, 0.3705, 0.3705],
          [0.0565, 0.0565, 0.2834, 0.2834, 0.3705, 0.3705],
          [0.4337, 0.4337, 0.8775, 0.8775, 0.8109, 0.8109],
          [0.4337, 0.4337, 0.8775, 0.8775, 0.8109, 0.8109],
          [0.8081, 0.8081, 0.8048, 0.8048, 0.3552, 0.3552],
          [0.8081, 0.8081, 0.8048, 0.8048, 0.3552, 0.3552]]]])
In [8]: out.shape
Out[8]: torch.Size([1, 1, 6, 6])
In [9]: out=F.interpolate(x,scale_factor=3,mode='nearest')
In [10]: out
Out[10]: 
tensor([[[[0.0565, 0.0565, 0.0565, 0.2834, 0.2834, 0.2834, 0.3705, 0.3705, 0.3705],
          [0.0565, 0.0565, 0.0565, 0.2834, 0.2834, 0.2834, 0.3705, 0.3705, 0.3705],
          [0.0565, 0.0565, 0.0565, 0.2834, 0.2834, 0.2834, 0.3705, 0.3705, 0.3705],
          [0.4337, 0.4337, 0.4337, 0.8775, 0.8775, 0.8775, 0.8109, 0.8109, 0.8109],
          [0.4337, 0.4337, 0.4337, 0.8775, 0.8775, 0.8775, 0.8109, 0.8109, 0.8109],
          [0.4337, 0.4337, 0.4337, 0.8775, 0.8775, 0.8775, 0.8109, 0.8109, 0.8109],
          [0.8081, 0.8081, 0.8081, 0.8048, 0.8048, 0.8048, 0.3552, 0.3552, 0.3552],
          [0.8081, 0.8081, 0.8081, 0.8048, 0.8048, 0.8048, 0.3552, 0.3552, 0.3552],
          [0.8081, 0.8081, 0.8081, 0.8048, 0.8048, 0.8048, 0.3552, 0.3552, 0.3552]]]])
In [11]: out.shape
Out[11]: torch.Size([1, 1, 9, 9])

ReLU

卷积神经网络的ReLU函数和之前全连接神经网络所说的ReLU函数一样，在这里是被用于去除响应过小的点。

ReLU函数原理

PyTorch实现

和原来全连接神经网络使用的函数一模一样

1
2
3
4
5
6
7
8
9
10
11
In [3]: import torch.nn as nn
In [4]: import torch.nn.functional as F
In [5]: x=torch.rand(1,16,7,7)
In [6]: layer=nn.ReLU(inplace=True)
In [7]: out=layer(x)
In [8]: out.shape
Out[8]: torch.Size([1, 16, 7, 7])
In [9]: out=F.relu(x)
In [10]: out.shape
Out[10]: torch.Size([1, 16, 7, 7])

Batch-Norm（归一化）

norm其实归一化就是特征缩放（feature scaling），一般情况我们将特征缩放成以0为均值1为方差的情况。

Batch norm在卷积神经网络中是指，对所有样本的相同层进行归一化处理。

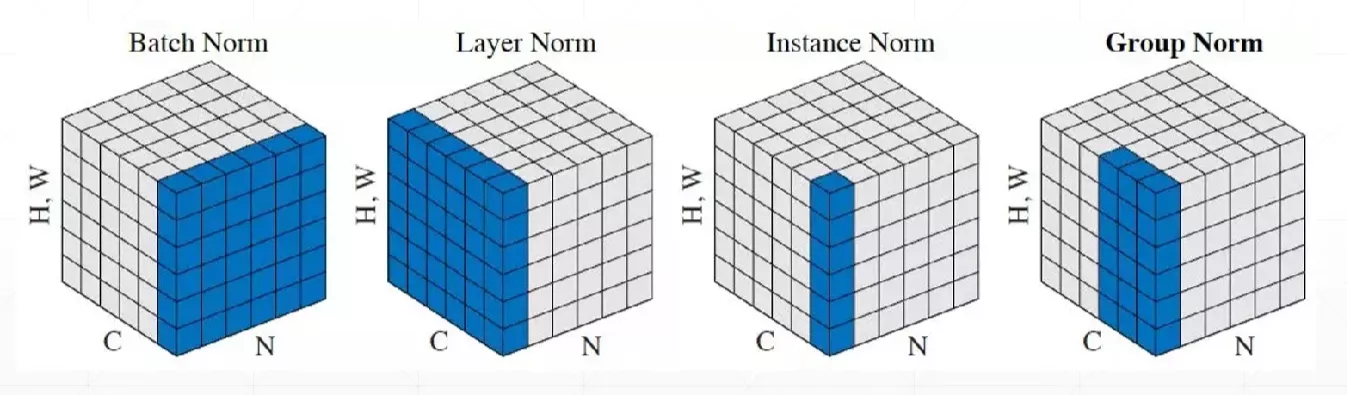
不同类型的norm原理图

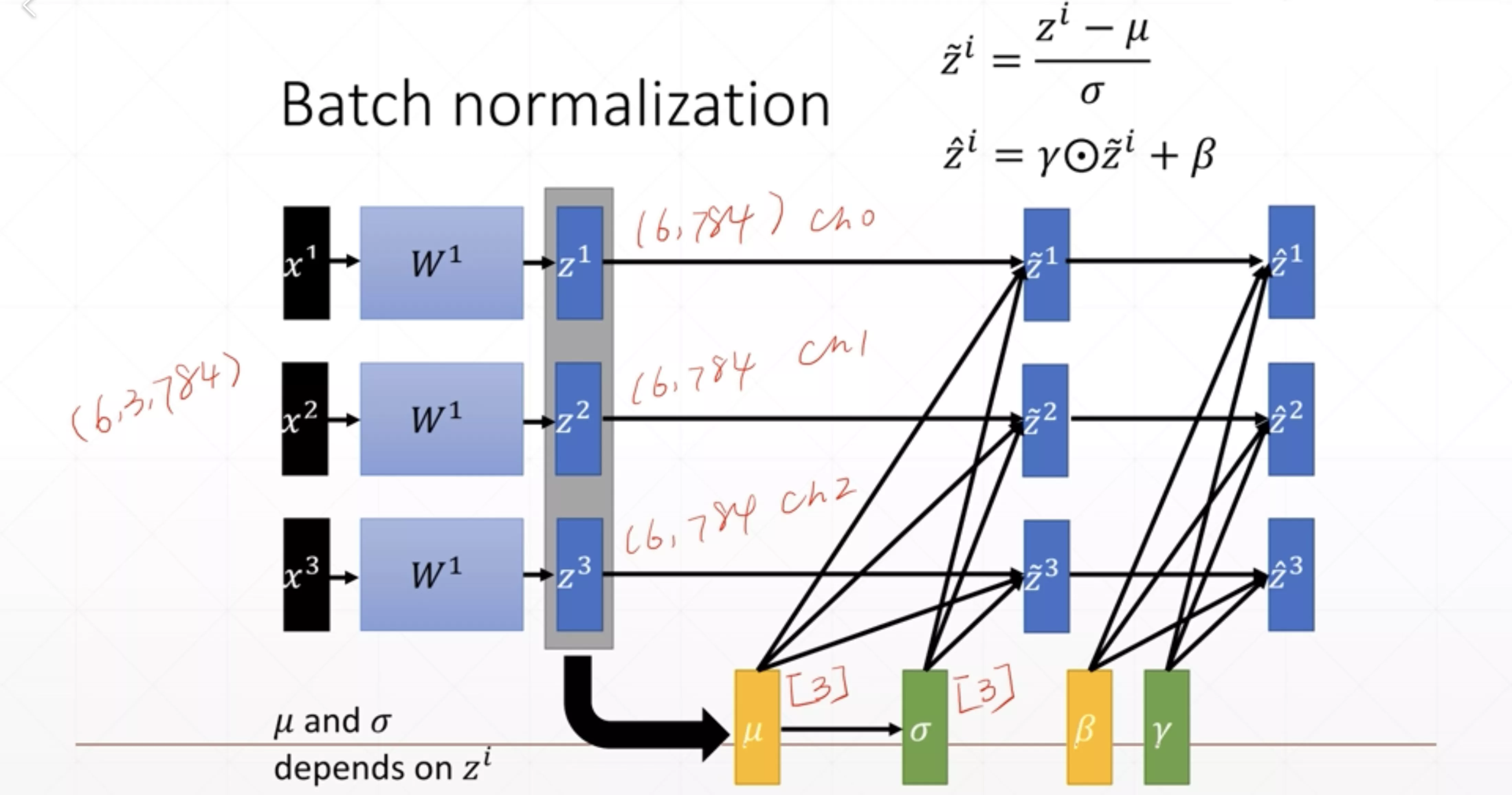
Batch norm 原理图

γ,β\gamma,\beta是要参与反向传播的，μ,α\mu,\alpha是不参与反向传播的，是运行中统计出来的数据。当前μ,α\mu,\alpha的计算也和上一次μ,α\mu,\alpha的值有关（指数加权平均）

PyTorch 实现

下面实现一个全连接层的Batchnorm，所使用的函数是torch.nn.BatchNorm1d,输入参数表示有多少个特征，在下面的例子中是有16个特征

1
2
3
4
5
6
7
8
9
10
11
12
13
14
In [3]: x=torch.rand(100,16)+0.5
In [4]: layer=torch.nn.BatchNorm1d(16)
In [5]: layer.running_mean,layer.running_var
Out[5]: 
(tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]),
 tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]))
In [6]: out=layer(x)
In [7]: layer.running_mean,layer.running_var
Out[7]: 
(tensor([0.0961, 0.0963, 0.1018, 0.1019, 0.1005, 0.1021, 0.1000, 0.1006, 0.0965,
         0.1005, 0.1054, 0.0996, 0.0940, 0.1024, 0.0938, 0.1022]),
 tensor([0.9089, 0.9086, 0.9073, 0.9105, 0.9075, 0.9087, 0.9068, 0.9079, 0.9096,
         0.9084, 0.9087, 0.9086, 0.9073, 0.9090, 0.9072, 0.9097]))

running_mean,running_var统计的是当前输入的数据的均值和方差的

可以发现running_mean一开始并没有直接到真实数据的均值，这就是因为每一次计算的均值和前一次的均值是有关系的缘故。所以当我们这样计算多次后running_mean才会逐渐接近真实的均值（见下面的代码）

1
2
3
4
5
6
7
8
9
10
11
12
In [3]: x=torch.randn(100,16)+0.5
In [4]: layer=torch.nn.BatchNorm1d(16) 
In [5]: for i in range(100): out=layer(x)
In [6]: layer.running_mean
Out[6]: 
tensor([0.5601, 0.4520, 0.2556, 0.4875, 0.4371, 0.3810, 0.4296, 0.4426, 0.5163,
        0.5468, 0.4442, 0.3907, 0.4959, 0.5350, 0.5775, 0.3721])
In [7]: layer.running_var
Out[7]: 
tensor([0.8751, 0.9497, 0.8256, 0.9304, 0.9371, 0.8656, 0.8312, 0.9728, 0.9176,
        0.9641, 1.2020, 0.8723, 1.3406, 0.8414, 0.9326, 0.9007])

下面我们进一步来看看BatchNorm对于2d的数据是如何进行操作的，这里所使用的函数是BatchNorm2d，参数代表的含义是有多少个通道。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
In [3]: import torch.nn as nn
In [4]: x=torch.randn(3,16,7,7)
In [5]: layer=nn.BatchNorm2d(16)
In [6]: out=layer(x)
In [7]: out.shape
Out[7]: torch.Size([3, 16, 7, 7])
In [8]: layer.weight
Out[8]: 
Parameter containing:
tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
       requires_grad=True)
In [9]: layer.bias
Out[9]: 
Parameter containing:
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
       requires_grad=True)
In [10]: layer.running_mean
Out[10]: 
tensor([-3.1731e-03, -1.3501e-03, -2.2491e-03,  9.6934e-05, -2.5191e-03,
        -4.5400e-03, -1.0107e-02,  1.9353e-03, -1.2692e-02,  8.8569e-03,
         9.0268e-04, -1.6005e-03, -8.5016e-03, -9.6128e-03,  1.5821e-03,
         1.9608e-02])
In [11]: layer.running_var
Out[11]: 
tensor([1.0157, 0.9935, 0.9906, 1.0245, 1.0056, 1.0123, 1.0102, 1.0013, 0.9842,
        0.9849, 0.9979, 0.9973, 1.0035, 0.9945, 0.9796, 1.0021])

`layer.weight`代表的是上面原理图中的$\gamma$,`layer.bias`代表的是上面原理图中的$\beta$，`layer.running_mean`代表的是$\mu$，`layer.running_var`代表的是

σ\sigma

使用vars可以打出层的所有信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
In [12]: vars(layer)
Out[12]: 
{'training': True,
 '_parameters': OrderedDict([('weight', Parameter containing:
               tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
                      requires_grad=True)),
              ('bias',
               Parameter containing:
               tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
                      requires_grad=True))]),
 '_buffers': OrderedDict([('running_mean',
               tensor([-3.1731e-03, -1.3501e-03, -2.2491e-03,  9.6934e-05, -2.5191e-03,
                       -4.5400e-03, -1.0107e-02,  1.9353e-03, -1.2692e-02,  8.8569e-03,
                        9.0268e-04, -1.6005e-03, -8.5016e-03, -9.6128e-03,  1.5821e-03,
                        1.9608e-02])),
              ('running_var',
               tensor([1.0157, 0.9935, 0.9906, 1.0245, 1.0056, 1.0123, 1.0102, 1.0013, 0.9842,
                       0.9849, 0.9979, 0.9973, 1.0035, 0.9945, 0.9796, 1.0021])),
              ('num_batches_tracked', tensor(1))]),
 '_non_persistent_buffers_set': set(),
 '_backward_hooks': OrderedDict(),
 '_is_full_backward_hook': None,
 '_forward_hooks': OrderedDict(),
 '_forward_pre_hooks': OrderedDict(),
 '_state_dict_hooks': OrderedDict(),
 '_load_state_dict_pre_hooks': OrderedDict(),
 '_modules': OrderedDict(),
 'num_features': 16,
 'eps': 1e-05,
 'momentum': 0.1,
 'affine': True,
 'track_running_stats': True}

因为Batchnorm层在训练模式和测试模式下的行为有所差别，所以在进行测试时，要使用eval把Batchnorm层的状态转换过来（从训练模式转换为测试模式）。因为test的时候只有一个样本，所以μ,σ2\mu,\sigma^2是无法被统计的。一般这个时候这两个值会被赋值为全局的值。

合理使用BatchNorm可以加快收敛速度并且提高准确度，而且使用了以后模型的鲁棒性会提升（模型更加稳定）

经典的卷积神经网络

经典CNN错误率比较

其中几个转折点

  • AlexNet(2012)
  • ZFNet(2013)
  • VGG(2014)
  • GoogLeNet(2014)
  • ResNet※

LeNet-5

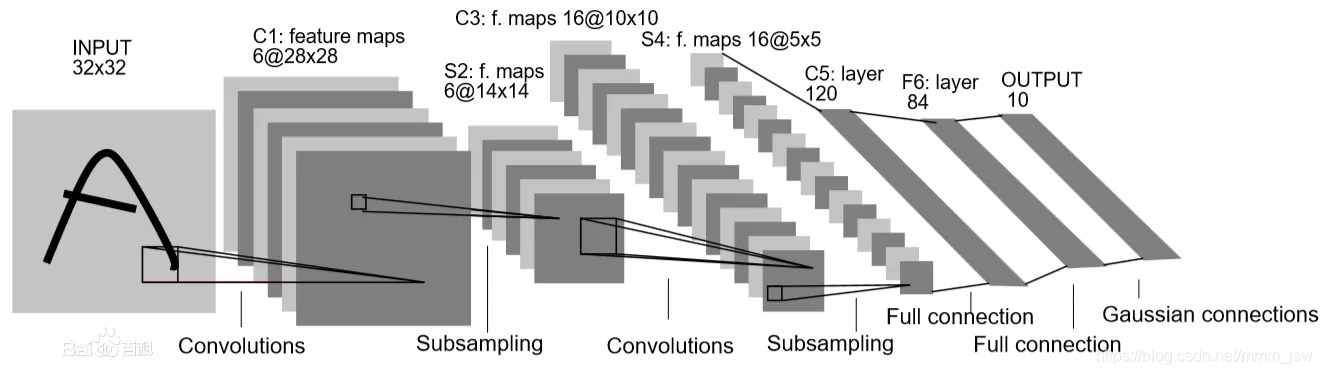
LeNet由Yann Lecun 提出，是一种经典的卷积神经网络，是现代卷积神经网络的起源之一。Yann将该网络用于邮局的邮政的邮政编码识别，有着良好的学习和识别能力。LeNet又称LeNet-5,具有一个输入层，两个卷积层，两个池化层，3个全连接层（其中最后一个全连接层为输出层）。

LeNet-5是一种经典的卷积神经网络结构，于1998年投入实际使用中。该网络最早应用于手写体字符识别应用中。普遍认为，卷积神经网络的出现开始于LeCun 等提出的LeNet 网络（LeCun et al., 1998），可以说LeCun 等是CNN 的缔造者，而LeNet-5 则是LeCun 等创造的CNN 经典之作 。

Yann Lecun

网络结构如下图所示，先是一个卷积层，然后是一个下采样，然后又是一个卷积层，然后又是一个下采样，最后三个就是三个全连接层。

LeNet-5

AlexNet

AlexNet

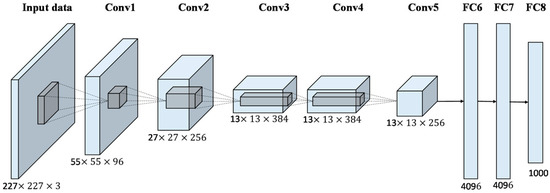
AlexNet是2012年ImageNet竞赛冠军获得者Hinton和他的学生Alex Krizhevsky设计的。也是在那年之后，更多的更深的神经网络被提出，比如优秀的VGG，GoogLeNet。 这对于传统的机器学习分类算法而言，已经相当的出色。

AlexNet中包含了几个比较新的技术点，也首次在CNN中成功应用了ReLU、Dropout和LRN等Trick。同时AlexNet也使用了GPU进行运算加速。

AlexNet将LeNet的思想发扬光大，把CNN的基本原理应用到了很深很宽的网络中。AlexNet主要使用到的新技术点如下：

（1）成功使用ReLU作为CNN的激活函数，并验证其效果在较深的网络超过了Sigmoid，成功解决了Sigmoid在网络较深时的梯度弥散问题。虽然ReLU激活函数在很久之前就被提出了，但是直到AlexNet的出现才将其发扬光大。

（2）训练时使用Dropout随机忽略一部分神经元，以避免模型过拟合。Dropout虽有单独的论文论述，但是AlexNet将其实用化，通过实践证实了它的效果。在AlexNet中主要是最后几个全连接层使用了Dropout。

（3）在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化，AlexNet全部使用最大池化，避免平均池化的模糊化效果。并且AlexNet中提出让步长比池化核的尺寸小，这样池化层的输出之间会有重叠和覆盖，提升了特征的丰富性。

（4）提出了LRN层，对局部神经元的活动创建竞争机制，使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。

（5）使用CUDA加速深度卷积网络的训练，利用GPU强大的并行计算能力，处理神经网络训练时大量的矩阵运算。AlexNet使用了两块GTX 580 GPU进行训练，单个GTX 580只有3GB显存，这限制了可训练的网络的最大规模。因此作者将AlexNet分布在两个GPU上，在每个GPU的显存中储存一半的神经元的参数。因为GPU之间通信方便，可以互相访问显存，而不需要通过主机内存，所以同时使用多块GPU也是非常高效的。同时，AlexNet的设计让GPU之间的通信只在网络的某些层进行，控制了通信的性能损耗。

（6）数据增强，随机地从256256的原始图像中截取224224大小的区域（以及水平翻转的镜像），相当于增加了2*(256-224)^2=2048倍的数据量。如果没有数据增强，仅靠原始的数据量，参数众多的CNN会陷入过拟合中，使用了数据增强后可以大大减轻过拟合，提升泛化能力。进行预测时，则是取图片的四个角加中间共5个位置，并进行左右翻转，一共获得10张图片，对他们进行预测并对10次结果求均值。同时，AlexNet论文中提到了会对图像的RGB数据进行PCA处理，并对主成分做一个标准差为0.1的高斯扰动，增加一些噪声，这个Trick可以让错误率再下降1%。

模型特点

  • 使用了ReLU激活函数
  • 使用了最大池化层
  • 标准化
  • Dropout

VGG

VGG

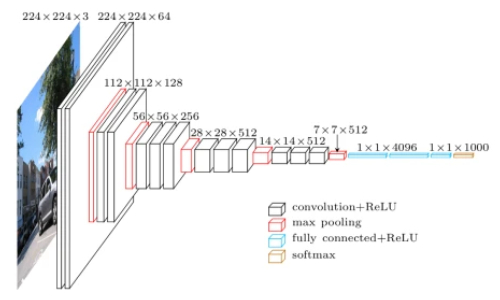
VGG模型是2014年ILSVRC竞赛的第二名，第一名是GoogLeNet。但是VGG模型在多个迁移学习任务中的表现要优于GoogLeNet。而且，从图像中提取CNN特征，VGG模型是首选算法。它的缺点在于，参数量有140M之多，需要更大的存储空间。但是这个模型很有研究价值。

模型的名称——“VGG”代表了牛津大学的Oxford Visual Geometry Group，该小组隶属于1985年成立的Robotics Research Group，该Group研究范围包括了机器学习到移动机器人。下面是一段来自网络对同年GoogLeNet和VGG的描述：

“GoogLeNet和VGG的Classification模型从原理上并没有与传统的CNN模型有太大不同。大家所用的Pipeline也都是：训练时候：各种数据Augmentation（剪裁，不同大小，调亮度，饱和度，对比度，偏色），剪裁送入CNN模型，Softmax，Backprop。测试时候：尽量把测试数据又各种Augmenting（剪裁，不同大小），把测试数据各种Augmenting后在训练的不同模型上的结果再继续Averaging出最后的结果。”

需要注意的是，在VGGNet的6组实验中，后面的4个网络均使用了pre-trained model A的某些层来做参数初始化。虽然提出者没有提该方法带来的性能增益。先来看看VGG的特点：

  • 小卷积核。作者将卷积核全部替换为3x3（极少用了1x1）；
  • 小池化核。相比AlexNet的3x3的池化核，VGG全部为2x2的池化核；
  • 层数更深特征图更宽。基于前两点外，由于卷积核专注于扩大通道数、池化专注于缩小宽和高，使得模型架构上更深更宽的同时，计算量的增加放缓；
  • 全连接转卷积。网络测试阶段将训练阶段的三个全连接替换为三个卷积，测试重用训练时的参数，使得测试得到的全卷积网络因为没有全连接的限制，因而可以接收任意宽或高为的输入。

GoogLeNet

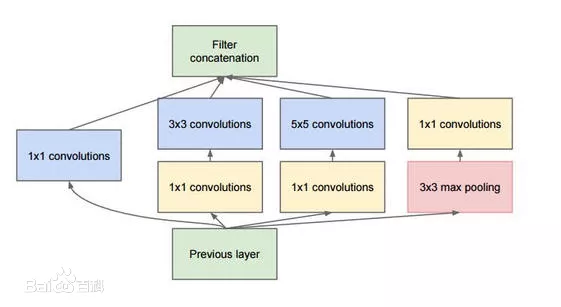
GoogLeNet

GoogLeNet是2014年Christian Szegedy提出的一种全新的深度学习结构，在这之前的AlexNet、VGG等结构都是通过增大网络的深度（层数）来获得更好的训练效果，但层数的增加会带来很多负作用，比如overfit、梯度消失、梯度爆炸等。inception的提出则从另一种角度来提升训练结果：能更高效的利用计算资源，在相同的计算量下能提取到更多的特征，从而提升训练结果。

模型特点

  • 使用不同大小的卷积核，从而感受不同范围的视野

ResNet（深度残差网络）※

这里单独将ResNet新开一个章节，已经表明了他在这一领域的重要性。首先来看看ResNet在2015年的战绩：

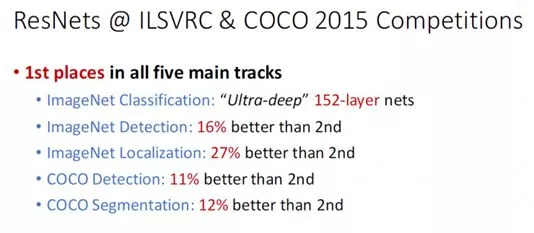
ResNet战绩

从经验来看，网络的深度对模型的性能至关重要，当增加网络层数后，网络可以进行更加复杂的特征模式的提取，所以当模型更深时理论上可以取得更好的结果，但是更深的网络其性能一定会更好吗？实验发现深度网络出现了退化问题（Degradation problem）：网络深度增加时，网络准确度出现饱和，甚至出现下降。56层的网络比20层网络效果还要差。这不会是过拟合问题，因为56层网络的训练误差同样高。我们知道深层网络存在着梯度消失或者爆炸的问题，这使得深度学习模型很难训练。但是现在已经存在一些技术手段如BatchNorm来缓解这个问题。因此，出现深度网络的退化问题是非常令人诧异的。但是何恺明发明的ResNet有效的解决了这一问题。ResNet有效解决了深度CNN模型难训练的问题（网络太深了容易发生梯度弥散）

ResNet残差网络主要是通过残差块组成的，在提出残差网络之前，网络结构无法很深，在VGG中，卷积网络达到了19层，在GoogLeNet中，网络达到了22层。随着网络层数的增加，网络发生了退化（degradation）的现象：随着网络层数的增多，训练集loss逐渐下降，然后趋于饱和，当你再增加网络深度的话，训练集loss反而会增大。而引入残差块后，网络可以达到很深，网络的效果也随之变好。

这里提供了一种想法：既然深层网络相比于浅层网络具有退化问题，那么是否可以保留深层网络的深度，又可以有浅层网络的优势去避免退化问题呢？如果将深层网络的后面若干层学习成恒等映射 h(x)=xh(x)=x ，那么模型就退化成浅层网络。但是直接去学习这个恒等映射是很困难的，那么就换一种方式，把网络设计成：

H(x)=F(x)+x⇒F(x)=H(x)−xH(x)=F(x)+x \Rightarrow F(x)=H(x)-x

只要 F(x)=0F(x)=0 就构成了一个恒等映射 H(x)=xH(x)=x ，这里 F(x)F(x) 为残差。

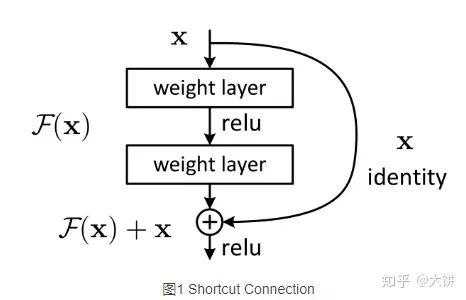
ResNet结构

相关资料链接：深度学习之16——残差网络(ResNet)

PyTorch 残差块实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class ResBlk(nn.Module):
    def __init__(self,ch_in,ch_out):
        self.conv1=nn.Conv2d(ch_in,ch_out,kernel_size=3,stride=1,padding=1)
        self.bn1=nn.BatchNorm2d(ch_out)
        self.conv2=nn.Conv2d(ch_in,ch_out,kernel_size=3,stride=1,padding=1)
        self.bn2=nn.BatchNorm2d(ch_out)

        self.extra=nn.Sequential()
        if ch_out!=ch_in: # 如果输入输出通道数量不一样的话
            self.extra!=ch_in:
            self.extra=nn.Sequential(
                nn.Conv2d(ch_in,ch_out,kernel_size=1,stride=1),
                nn.BatchNorm2s(ch_out)
            )
    def forward(self,x):
        out=F.relu(self.bn1(self.conv1(x)))
        out=self.bn2(self.conv2(out))
        out=self.extra(x)+out
        return out

DenseNet

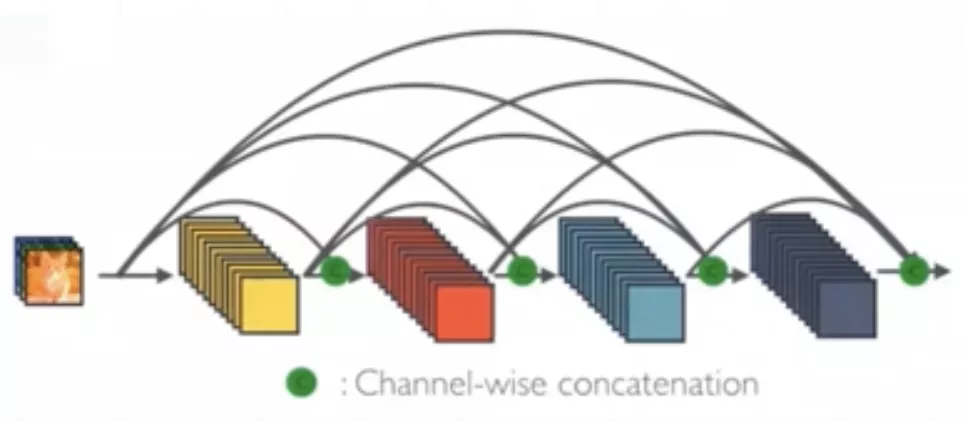
DenseNet结构图

其实相当于每一层都和前面所有层之间又一个shortcut

nn.Module

PyTorch中的nn.Module类为所有我们自定义网络层的一个父类！所以他非常的重要，以下是他的优点

提供了很多的操作

  • nn.Linear

  • nn.BatchNorm2d

  • nn.Conv2d

etc.

提供容器nn.Sequential

对网络参数能够进行很好的管理

下面举一个例子，我们采用的是一个两层的网络，所以参数有4组，weight0，bias0,weight1,bias1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
In [3]: import torch.nn as nn
In [4]: net=nn.Sequential(nn.Linear(4,2),nn.Linear(2,2))
In [5]: dict(net.named_parameters()).items()
Out[5]: 
dict_items([('0.weight', Parameter containing:
tensor([[-0.1411,  0.2698,  0.0457, -0.2939],
        [-0.3555, -0.3352, -0.3403,  0.4714]], requires_grad=True)), ('0.bias', Parameter containing:
tensor([ 0.1076, -0.1325], requires_grad=True)), ('1.weight', Parameter containing:
tensor([[ 0.0859, -0.6313],
        [-0.6823, -0.5285]], requires_grad=True)), ('1.bias', Parameter containing:
tensor([ 0.6793, -0.1800], requires_grad=True))])
In [6]: list(net.parameters())[0]
Out[6]: 
Parameter containing:
tensor([[-0.1411,  0.2698,  0.0457, -0.2939],
        [-0.3555, -0.3352, -0.3403,  0.4714]], requires_grad=True)
In [7]: list(net.parameters())[1]
Out[7]: 
Parameter containing:
tensor([ 0.1076, -0.1325], requires_grad=True)
In [8]: optimizer=optim.SGD(net.parameters(),lr=1e-3)

可以清晰的查看网络结构

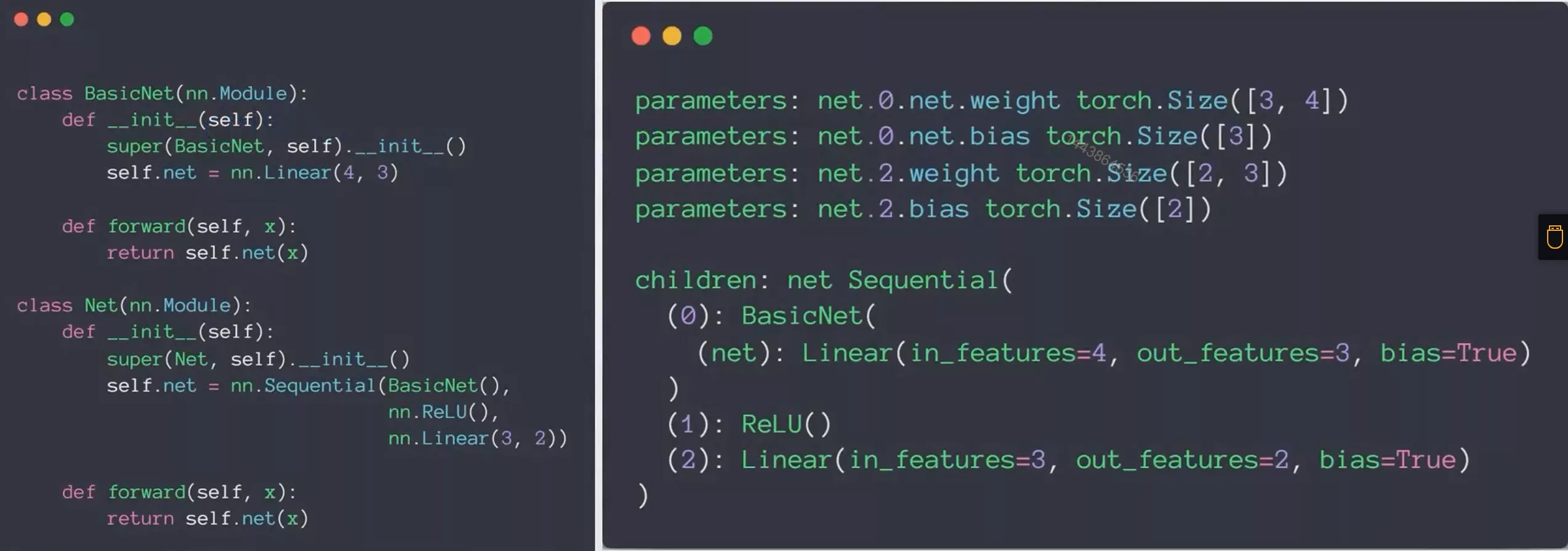
网络结构查看清晰

可以将网络方便的转移到GPU上进行加速

1
2
3
device=torch,device('cuda')
net=Net()
net.to(device)

可以很方便的保存和加载网络的中间状态

这就方便我们进行early stop

1
2
3
4
5
6
7
8
9
device=torch,device('cuda')
net=Net()
net.to(device)

net.load_state_dict(torch.load('ckpt.mdl')) # 加载模型

# train...

torch.save(net.state_dict(),'ckpt.mdl') # 保存模型

方便切换网络状态

对于网络中的一些层，比如BatchNorm层，他在训练状态下和测试状态下的行为是有一些差异的，如果我们对网络中的每一层都去执行切换状态的操作是非常麻烦的，但是nn.Module支持对自定义网络整体状态的切换，大大简化了操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
device = torch.device('cuda')
net=Net()
net.to(device)

# train
net.train()
# ...
# ...
# ...

# test
net.eval()
# ...

方便定义自己的类

比如说PyTorch现目前暂时不提供将tensor拍平的操作（层之间，作用是将卷积层转化为全连接层），因此这个层需要我们自己去实现

1
2
3
4
5
class Flatten(nn.Module):
    def __init__(self):
        super(Flatten,self).__init__()
    def forward(self,input):
        return input.view(input.size(0),-1)

以上这个类使用的非常的广泛

我们也可以尝试自己写一个Linear类

1
2
3
4
5
6
7
8
9
10
11
12
class MyLinear(nn.Module):
    
    def __init__(self,inp,outp):
        super(MyLinear,self).__init__()
        
        # requiers_grad = True
        self.w = nn.Parameter(torch.randn(outp,inp))
        self.b = nn.Parameter(torch.randn(outp))
    
    def forward(self, x):
        x = x @ self.w.t() + self.b
        return x

数据增强

其实非常好理解，数据增强让有限的数据产生更多的数据，增加训练样本的数量以及多样性（噪声数据），提升模型鲁棒性，一般用于训练集。神经网络需要大量的参数，许许多多的神经网路的参数都是数以百万计，而使得这些参数可以正确工作则需要大量的数据进行训练，但在很多实际的项目中，我们难以找到充足的数据来完成任务。随机改变训练样本可以降低模型对某些属性的依赖，从而提高模型的泛化能力。

常用的数举增强方法有

  • 翻转
  • 旋转
  • 随机移动和裁剪
  • 加噪
  • GAN

数据增强

翻转（Flip）

翻转

PyTorch 实现

1
2
3
4
5
6
7
8
9
10
train_loader=torch.utils.dataDataLoader(
    datasets.MNIST('../data',train=True,download=True,
                  	transform=transforms.Compose([
                        transforms.RandomHorizontalFlip(),# 因为前面是random，所以该操作有可能做也可能不做
                        transforms.RandomVerticalFlip(),
                        transforms.ToTensor(),
                        # transforms.Normalize((0.1307,),(0.3081,))
                    ])),
    batch_size=batch_size,shuffle=True
)

transform是torchvision中提供的操作

旋转（Rotate）

旋转

PyTorch实现

1
2
3
4
5
6
7
8
9
10
11
12
train_loader=torch.utils.dataDataLoader(
    datasets.MNIST('../data',train=True,download=True,
                  	transform=transforms.Compose([
                        transforms.RandomHorizontalFlip(),
                        transforms.RandomVerticalFlip(),
                        transforms.RandomRotation(15),# 这里是对于每张照片随机旋转一个角度，角度的范围是从-15°到15°
                        transforms.(RandomRotation([90,180,270]))# 这里是对于每张照片随机旋转一个角度，角度是 90°或180°或270°
                        transforms.ToTensor(),
                        # transforms.Normalize((0.1307,),(0.3081,))
                    ])),
    batch_size=batch_size,shuffle=True
)

缩放（scale）

缩放

PyTorch 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
train_loader=torch.utils.dataDataLoader(
    datasets.MNIST('../data',train=True,download=True,
                  	transform=transforms.Compose([
                        transforms.RandomHorizontalFlip(),
                        transforms.RandomVerticalFlip(),
                        transforms.RandomRotation(15),
                        transforms.(RandomRotation([90,180,270]))
                        transforms.Resize([32,32]) # 将大小变为32×32
                        transforms.ToTensor(),
                        # transforms.Normalize((0.1307,),(0.3081,))
                    ])),
    batch_size=batch_size,shuffle=True
)

随机移动和裁剪（Crop part）

随机移动和裁剪

PyTorch 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
train_loader=torch.utils.dataDataLoader(
    datasets.MNIST('../data',train=True,download=True,
                  	transform=transforms.Compose([
                        transforms.RandomHorizontalFlip(),
                        transforms.RandomVerticalFlip(),
                        transforms.RandomRotation(15),
                        transforms.(RandomRotation([90,180,270]))
                        transforms.Resize([32,32]) # 将大小变为32×32
                        transforms.ToTensor(),
                        transforms.RandomCrop([28,28])
                        # transforms.Normalize((0.1307,),(0.3081,))
                    ])),
    batch_size=batch_size,shuffle=True
)

一般进行数据增强是RandomRotation和RandomCrop结合起来一起使用的

加噪（Noise）

加噪

总结

虽然数据增强确实可以提高模型的表现，但是他不会帮助太多。

本站由 @anonymity 使用 Stellar 主题创建。
本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。